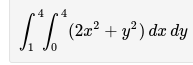Integration

Multi

Iterated Integrals

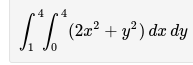
• Work from the inside out
• Partial Derivative but backwards
• Desmos Got that

Surface Integrals

Switching order of integration

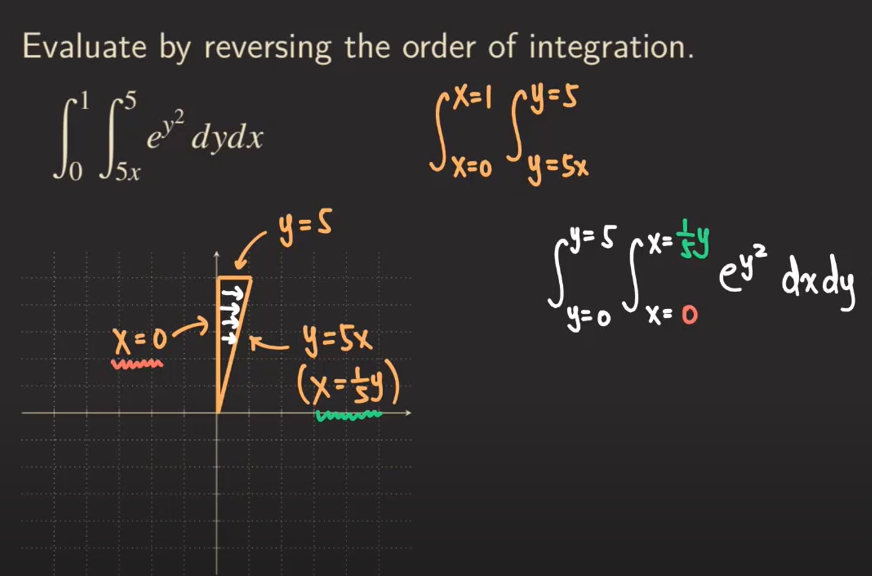
Integration by parts

$$\int f(x)\ast g^{\prime }(x)dx=f(x)g(x)-\int f^{\prime }(x)g(x)dx$$

• Find an f(x) where deriving simplifies it
• Find a g’(x) where anti deriving doesn’t make it more complicated

Simple Example

$${\int }_0^{\pi }xcos(x)dx$$

• x becomes simpler when derived, so is f(x)

$$f(x)=x$$ $$f^{\prime }(x)=1$$

• cos(x) anti derivative doesn’t get more complicated, so it’s g(x)

$$g^{\prime }(x)=sin(x)$$ $$g(x)=sin(x)$$

• And so we get things which we can substitute into the formula

$$x\ast sin(x)-\int 1sin(x)dx$$ $$x\ast sin(x)+\int -sin(x)dx$$ $$x\ast sin(x)+cos(x)dx$$ $$x\ast sin(x)+cos(x){|}_0^{\pi }$$

More Examples

---

$${\int }_1^e\frac{-2ln(x)}{x^2}$$ $$f(x)=-2ln(x)$$ $$f^{\prime }(x)=\frac{-2}{x}$$ $$g^{\prime }(x)=\frac{1}{x^2}$$ $$g(x)=-\frac{1}{x}$$ $$-2ln(x)\ast -\frac{1}{x}-\int \frac{-2}{x}\ast -\frac{1}{x}dx$$ $$-2ln(x)\ast -\frac{1}{x}+\frac{2}{x}$$ $$-2ln(x)\ast -\frac{1}{x}+\frac{2}{x}{|}_1^e$$

---

$$\int 7xsin(x)$$ $$f(x)=7x$$ $$f^{\prime }(x)=7$$ $$g^{\prime }(x)=sin(x)$$ $$g(x)=-cos(x)$$ $$7x\ast -cos(x)-\int 7\ast -cos(x)$$ $$7x\ast -cos(x)+\int 7\ast cos(x)$$ $$-7xcos(x)+7sin(x)$$

---

$${\int }_1^4{t}^{2}ln(5t)dt$$ $$f(t)=ln(5t)$$ $$f^{\prime }(t)=1/t$$ $$g^{\prime }(t)=t^2$$ $$g(x)=\frac{t^3}{3}$$ $$ln(5t)\frac{t^3}{3}-\int \frac{1}{t}\frac{t^3}{3}dx$$ $$ln(5t)\frac{t^3}{3}-\int \frac{t^2}{3}dx$$ $$ln(5t)\frac{t^3}{3}-\frac{t^3}{9}$$

---

$${\int }_1^2\frac{ln(r)}{r^3}$$ $$f(x)=ln(r)$$ $$f^{\prime }(x)=1/x$$ $$g^{\prime }(x)=r^{-3}$$ $$g(x)=\frac{r^{-2}}{-2}$$ $$ln(r)\frac{r^{-2}}{-2}-\int \frac{1}{x}\frac{r^{-2}}{-2}$$ $$ln(r)\frac{r^{-2}}{-2}-\int \frac{r^{-2}}{-2x}$$ $$ln(r)\frac{r^{-2}}{-2}-\frac{1}{4r^2}$$

Maybe wrong skull

---

$$ln(x)\sqrt{x^{11}}$$ $$f(x)=ln(x)$$ $$f^{\prime }(x)=1/x$$ $$g^{\prime }(x)=x^{11/2}$$ $$g(x)=x^{9/2}/(11/2)$$

?????