- (3 pts) Under what condition is the total angular momentum of a system conserved?
- (3 pts) If the Earth can be considered a uniform sphere with mass 5.97 * 10^24 kg and a radius of 6.37 * 10^3 kg, determine its moment of inertia.
- (6 pts) The Earth completes one rotation every 23.9 hours. Determine:
a) its angular speed
b) its angular momentum
c) and its kinetic energy. Report the kinetic energy in jules.
- A hole is drilled at the center of a 3.00 m long thin rod with a mass of 4.00 kg. The rod is mounted to a fixed axle through the hole (center of the rod). A 2.00 kg piece of clay is placed at one end of the rod as shown in the figure. From a horizontal position, the rod is released from rest.
a) (3 pts) What is the moment of inertia of the rod-clay system for rotation about the center of the rod?
b) (3 pts) How far is the center-of-mass of the system from the axle?
c) (6 pts) If there is no friction at the axle and air resistance can be neglected, what will be the angular speed of the rod when it passes through the vertical?

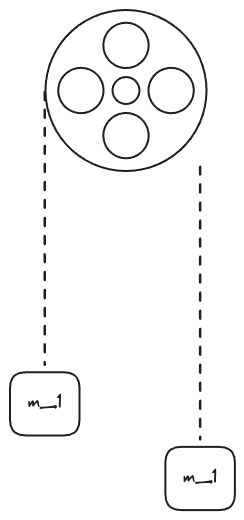
- (12 pts) A mass is attached to each end of a string passing over a pulley as shown. The pulley has a radius of 0.1 m, but is not a uniform solid cylinder. The mass m_1 = 6.00 kg includes a force sensor that can measure the tension in the in the string pulling it upward. The mass m_2 = 8.00 kg is released from rest. As m_2 travels downward, the force sensor reads 63.0 N. Determine the moment of inertia of the pulley.
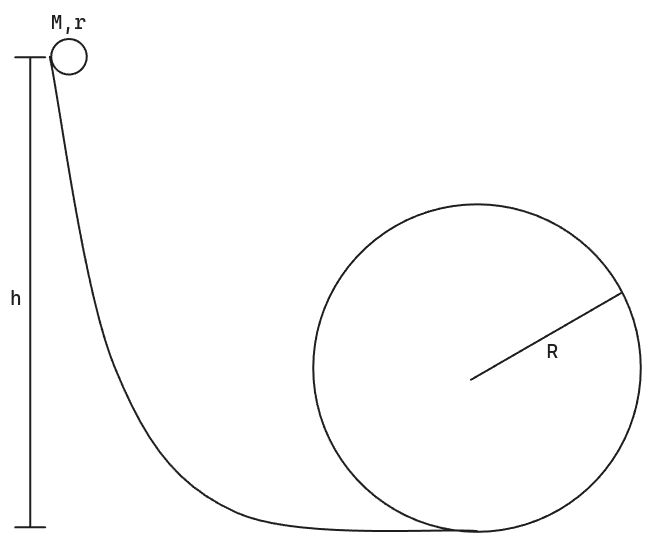
- (12 pts) Suppose you use a solid glass sphere with a loop track. The sphere has a radius r and and a mass M. The loop track has a radius R. If the sphere is released from rest a distance h=3R, determine the magnitude of the normal force on the sphere as it passes the highest point on the loop. Your answer should be in terms of M, R, r, g, and numerical constants.
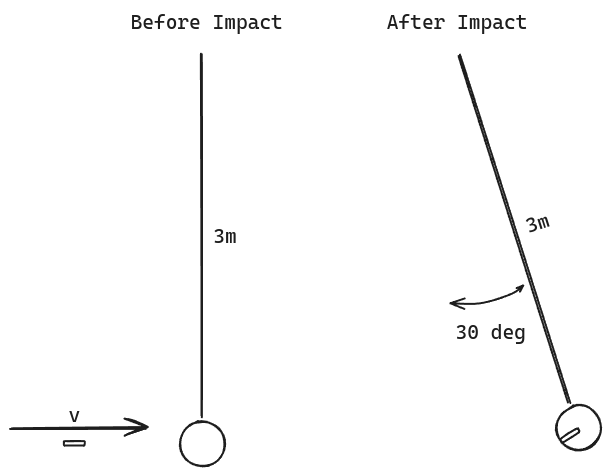
- (12 pts) To determine the speed of a 25.0 g bullet, a 525 g sphere is hung from a 3.00 m long string. The bullet is fired horizontally into the sphere. The bullet becomes embedded in the sphere and they swing to a maximum angle of 30.0 degrees from the vertical. Determine the initial speed of the bullet.