Exam 2 Review

Motorized Cart

A crate on a motorized cart starts from rest and moves with a constant eastward acceleration of $A=2.60m/s^2$ . A worker assists the cart by pushing on the crate with a force that is eastward and has magnitude that depends on time according to $F(t)=(5.40N/s)t$

What is the instantaneous power supplied by this force at $t=4.60s$ ?

Solution:

Work in Jules is the same as change in kinetic energy or $\Delta K$, so long as force and distance are straight:
Kinematics Equations:

$$\Delta K(J)=Fdcos(\theta )$$

Since force and distance are both parallel and pointed in the same direction:

$$\Delta K(J)=Fd$$

SI unit for instantaneous power is Watts, $W=J/s$. Since force is instantaneous, we simply need to find the instantaneous change in distance.. velocity
Kinematics Equations:

$$x=x_0+V_{0x}t+0.5A_x{t}^2$$

Starting position is irrelevant since we will be deriving this, initial velocity is zero

$$x=0.5A_x{t}^2$$

Substitute:

$$x=0.5(2.6)t^2$$

Derive:

$$x=(2.6)t$$

Substitute back into $\Delta K$ Equation:

$$P(W)=\frac{\Delta K}{\Delta t}=2.6t\ast 5.4t$$

Solve when t=4.6s:

$$P(W)=\frac{\Delta K}{\Delta t}=297.08$$

“Unfaithful Spring” (Spring with arbitrary force function)

Consider a spring that does not obey Hooke’s law very faithfully. One end of the spring is fixed. To keep the spring stretched or compressed an amount $x$, a force along the $x$-axis with $x$-component $F_x=kx-b{x}^2+c{x}^3$ must be applied to the free end. Here $k=100N/m$, $b=700N/m^2$, and $c=12000N/m^3$. Note that $x>0$ when the spring is stretched and $x<0$ when it is compressed.

How much work must be done to stretch this spring by 0.050 mm from its unstretched length?

How much work must be done to compress this spring by 0.050 mm from its unstretched length?

Solution

We know from the work and energy equations that the integral of force over distance is work:

$$W={\int }_A^B\vec{F}\cdot d\vec{l}$$

Substitute in $F_x(x)$ and adjust integration variable (we can also turn this into scalars because the force and displacement are aligned):

$$W={\int }_A^{B}kx-b{x}^2+c{x}^{3}dx$$

Integrate:

$$W=\frac{k{x}^2}{2}-\frac{b{x}^3}{3}+\frac{c{x}^4}{4}{|}_A^B$$

Part A (Stretch)

Substitute limits of integration:

$$W_s=\frac{k{x}^2}{2}-\frac{b{x}^3}{3}+\frac{c{x}^4}{4}{|}_0^{0.05}$$

Solve in Desmos:

$$W_s=0.115J$$

Part B (Compress)

Substitute limits of integration:

$$W_c=\frac{k{x}^2}{2}-\frac{b{x}^3}{3}+\frac{c{x}^4}{4}{|}_0^{-0.05}$$

Solve in Desmos:

$$W_c=0.173J$$

Spring Gun

The spring of a spring gun has force constant $k=400N/m$ and negligible mass. The spring is compressed $6.00cm$ and a ball with mass $0.0300kg$ is placed in the horizontal barrel against the compressed spring. The spring is then released, and the ball is propelled out the barrel of the gun. The barrel is $6.00cm$ long, so the ball leaves the barrel at the same point that it loses contact with the spring. The gun is held so the barrel is horizontal.

Calculate the speed with which the ball leaves the barrel if you can ignore friction.

Calculate the speed of the ball as it leaves the barrel if a constant resisting force of $6.00N$ acts on the ball as it moves along the barrel.

For the situation in part B, at what position along the barrel does the ball have the greatest speed? (In this case, the maximum speed does not occur at the end of the barrel.)

What is that greatest speed?

Solution

We know from the work and energy equations that the integral of force over distance is work:

$$W={\int }_A^B\vec{F}\cdot d\vec{l}$$

We know $F$ according to Hookes law:

$$F=lk$$

Substitute hookes law into work equation, dropping vector details because force and displacement are paralell:

$$W={\int }_A^{B}kxdx$$

Part A

Integrate and substitute limits of integration:

$$W=\frac{1}{2}k{x}^2{|}_0^{0.06}$$

Solve:

$$W=0.72J$$

We know from the work and energy equations:

$$K=0.5m{v}^2$$

Rework to:

$$v=\sqrt{\frac{2K}{m}}$$

Substitute work done by spring as kinetic energy of projectile, and mass:

$$v=\sqrt{\frac{2(0.72)}{0.03}}$$

Solve:

$$v=6.93m/s$$

Part B

There’s now $-6N$ of additional force, so we must rework from integral:

$$W={\int }_A^{B}kx-6dx$$ $$W=\frac{1}{2}k{x}^2-6x{|}_0^{0.06}$$

You don't necessarily have to re-integrate!

You could solve for the work done by the $-6N$ force separately, instead of re-integrating, but re-integrating works if the force isn’t constant over distance

Solve:

$$W=0.36J$$

We know from the work and energy equations:

$$K=0.5m{v}^2$$

Rework to:

$$v=\sqrt{\frac{2K}{m}}$$

Substitute work done by spring as kinetic energy of projectile, and mass:

$$v=\sqrt{\frac{2(0.35)}{0.03}}$$

Solve:

$$v=4.9m/s$$

Part C

Because the $-6N$ force is constant, we know the projectile will start slowing down when the spring force is plus the $-6N$ force equals 0, because after that point the $-6N$ force will be larger, the net force will be negative, and so will the acceleration of the projectile. In other words, find x when:

$$400x=6$$ $$x=0.015$$

Remember however that in hookes law, $x=0$ when the spring is at it’s natural extension, and in the problem (and in our equations… kinda), $x=0$ when the spring is fully compressed so:

$$x_{max}=0.06-0.015=0.45$$

Part D

We only need to rework part B’s limits of integration:

$$W=\frac{1}{2}k{x}^2-6x{|}_{0.015}^{0.06}$$

Solve:

$$W=0.405J$$

We know from the work and energy equations:

$$K=0.5m{v}^2$$

Rework to:

$$v=\sqrt{\frac{2K}{m}}$$

Substitute work done by spring as kinetic energy of projectile, and mass:

$$v=\sqrt{\frac{2(0.405)}{0.03}}$$

Solve:

$$v=5.2m/s$$

Car Going over Hill

A road heading due east passes over a small hill. You drive a car of mass mm at constant speed vv over the top of the hill, where the shape of the roadway is well approximated as an arc of a circle with radius RR. Sensors have been placed on the road surface there to measure the downward force that cars exert on the surface at various speeds. The table gives values of this force versus speed for your car is shown in the table below. Treat the car as a particle.

Speed (m/s)	6.00	8.00	10.0	12.0	14.0	16.0
Force (N)	8100	7690	7050	6100	5200	4200

Someone help me out??

A box on a Board on a Table

A small box of mass $m_1$ is sitting on a board of mass $m_2$ and length $L$. The board rests on a friction-less horizontal surface. The coefficient of static friction between the board and the box is $\mu s$. The coefficient of kinetic friction between the board and the box is, as usual, less than $\mu s$.

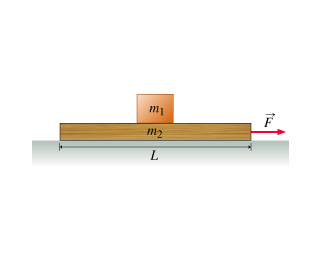
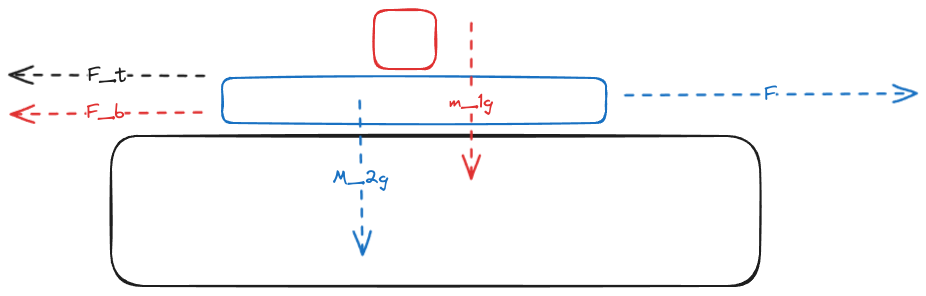
Solution

The box will start sliding when the force is bigger than the maximum static friction force of the box and the plank.

This maximum static friction force is:

$$f_{max}={\mu }_s{m}_{1}g$$

When the box and plank are accelerating together, their acceleration is given by $F_{net}=ma$:

$$a=\frac{F}{m_1+m_2}$$

Starting from the slip condition…

$$m_{1}a>\mu s{m}_{1}g$$

Substitute in equation for system acceleration:

$$m_1\frac{F}{m_1+m_2}>\mu s{m}_{1}g$$ $$F>{\mu }_{s}g(m_1+m_2)$$

So the minimum force where slippage will occur is:

$$F_{min}={\mu }_{s}g(m_1+m_2)$$

Pendulum Ball Tension Ratio

A ball is held at rest at position $A$ in the figure by two light strings. The horizontal string is cut and the ball starts swinging as a pendulum. Point $B$ is the farthest to the right the ball goes as it swings back and forth.

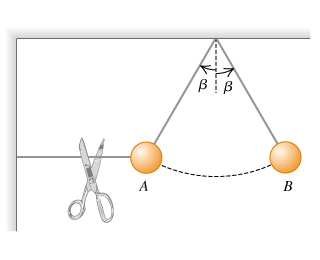
What is the ratio of the tension in the supporting string in position B to its value at A before the horizontal string was cut?

Solution

Tension Pre-Cut

$$mg=T_{s}cos(\beta )$$ $$T_s=\frac{mg}{cos(\beta )}$$

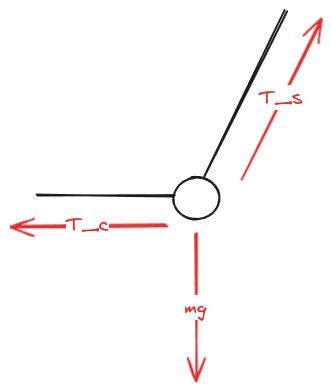
Tension At Apex Post-Cut

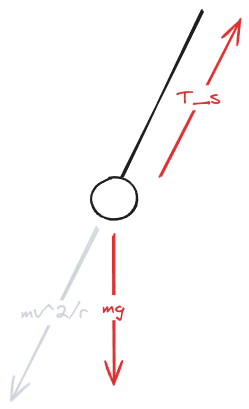
At first I thought that centripetal acceleration would need to be accounted, for, but at the apex, $v=0$, so it does not.

erm wut

https://www.youtube.com/watch?v=p8EcpFLEBQQ

$$T_s=mgcos(\beta )$$

Tension Ratio

$$T_b/T_a=cos(\beta {)}^2$$

Boxes linked by string on ramp

Two blocks connected by a cord passing over a small, frictionless pulley rest on frictionless planes

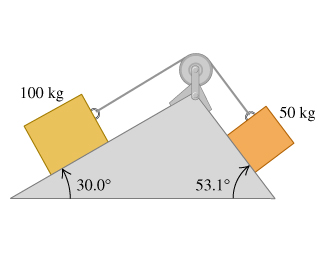
Solution

Tension on string by left block (when static)

$$T_L=100gcos(120)$$

Tension on string by right block (when static

$$T_R=50gcos(143.1)$$

Since $T_L>T_R$, The blocks will slide to the left

Acceleration
From $F_{net}=ma$, we get:

$$a=F/m$$

Net force (in relevant directions) will be $F_{net}=T_L-T_R$, Substituting:

$$a=\frac{100gcos(120)-T_R=50gcos(143.1)}{150}$$ $$a=0.65m/s^2$$

Tension in cord
It’s janky, but adding the acceleration to g when solving for tension in either block should work… just check your signs and make sure to consider the angle of the acceleration due to gravity is not the same as the acceleration direction of the block:

$$T=50((g)cos(143.1)+0.65)$$ $$T=420N$$

Stacked blocks sliding in opposite directions on a table

Consider two blocks connected. Block A has mass $2.00kg$, and block B has mass $5.00kg$. The table on which B sits is frictionless, the cord connecting the blocks is light and flexible, and the pulley is light and frictionless. The horizontal force $\vec{F}$ has magnitude $F=20.0N$, and block B moves to the left with an acceleration of $1.70m/s^2$ .

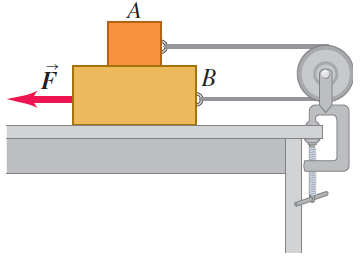
What is the tension in the cord that connects the two blocks?

What is the coefficient of kinetic friction that one block exerts on the other?

Fuck me: https://chatgpt.com/share/670243db-ba10-8011-b9a3-809af8a1ba9d
But thans Ihermie for the prompt engineering

And thanks acharmlet for the work

Tripple blocks dangly thing

Block A in the figure has a mass of $4.50kg$, and block B has mass $13.0kg$ . The coefficient of kinetic friction between block B and the horizontal surface is $0.25$.

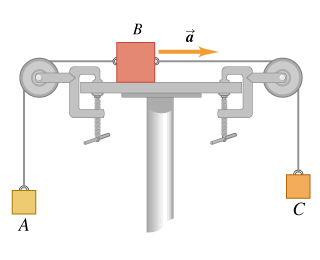
+x is to the right

$$F_{net}=ma$$ $$(m_a+m_b+m_c)a=g{m}_c-g{\mu }_k{m}_b-g{m}_a$$

Substitute:

$$(4.5+13+m_c)(2.4)=(9.81)m_c-(9.81)(0.25)(13)-(9.81)4.5$$ $$m_c=15.9kg$$

Tension AB

$$T_{AB}=m_a(g+a)$$ $$T_{AB}=4.5(9.81+2.4)$$ $$T_{AB}=54.945$$

Tension BC

$$T_{BC}=m_c(g-a)$$ $$T_{BC}=117.819$$