Moment of Inertia Lab

Data

Objects

Pulley: $r=0.0164m$
Disk:
Mass: $m_d=1.426kg$
Radius: $r_d=0.1115m$

Ring:
Mass: $m_r=1.429kg$
Inner Radius: $r_{ri}=0.0512m$
Outer Radius: $r_{ro}=0.0635m$

Experiment

System	Symbol	Horizontal Disk	Horizontal Disk + Ring	Vertical Disk
Friction Mass (kg)	$m_f$	$0.0055\pm 0.0005$	$0.0095\pm 0.0005$	$0.0055\pm 0.0005$
Driving Mass (kg)	$m$	$0.05$	$0.1$	$0.05$
Height (m)	$d$	$0.906$	$0.906$	$0.906$
Time 1 (s)		$22.1$	$19.1$	$16.5$
Time 2 (s)		$22.7$	$18.6$	$16.5$
Time 3 (s)		$22.2$	$17.6$	$16.4$
Avg Time (s)	$t$	$22.33$	$18.43$	$16.46$

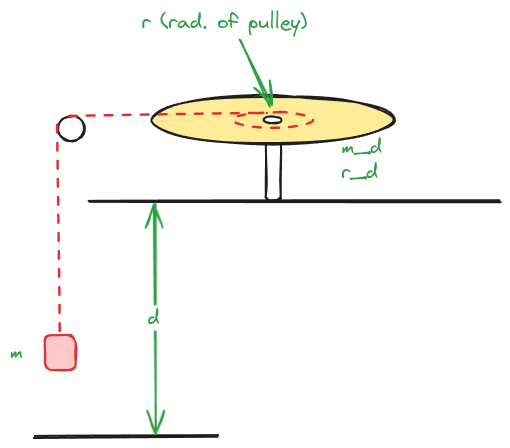
Diagram

Calculation of $v$ and $K_f$ for driving mass

Find Acceleration

$$x=x_0+V_{0x}t+0.5A_x{t}^2$$ $$d=0.5A_x{t}^2$$ $$a=\frac{2d}{t^2}$$ $$a=\frac{2(0.906)}{22.23^2}=0.003666m/s^2$$

Use $a$ to find final v

$$V_x^2=V_{0x}^2+2A_x(x-x_0)$$ $$v=\sqrt{2ad}$$

Substitute in equation for a:

$$v=\sqrt{2d\frac{2d}{t^2}}$$ $$v=\sqrt{\frac{4d^2}{t^2}}$$ $$v=\frac{2d}{t}$$ $$v=\frac{2(0.906)}{22.33}=0.081146$$

Find Kinetic Energy

$$K=0.5m{v}^2$$

Substitute:

$$K=0.5m\frac{4d^2}{t^2}$$ $$K=0.5(0.05)\frac{4(0.906{)}^2}{(22.33{)}^2}=0.00016461J$$

$K_{rot}$ Calculation

We know that the the work done by gravity on the driving mass (less friction) will be equal to the kinetic energy of the system.

$$W=K+K_{rot}$$

Effective mass (mass less friction mass):

$$m_e=m-m_f$$

Work done by gravity:

$$W=m_{e}gd$$

Substitute and solve for $K_{rot}$:

$$m_{e}gd=0.5m_e\frac{4d^2}{t^2}+K_{rot}$$ $$K_{rot}=m_{e}gd-0.5m_e\frac{4d^2}{t^2}$$ $$K_{rot}=(0.05-0.0055)(9.81)(0.906)-0.5(0.05-0.0055)\frac{4(0.906{)}^2}{(22.33{)}^2}=0.3954J$$

$\omega$ Calculation

Linear velocity, divided by circumference, multiplied by $2\pi$ comes out to:

$$\omega =\frac{v}{r}$$

Substituting:

$$\omega =\frac{(\frac{2d}{t})}{r}$$ $$\omega =\frac{(\frac{2(0.906)}{22.33})}{0.0082}=9.895rad/s=1.574rev/s$$

$I_{exD}$ Calculation

$$K=\frac{1}{2}I{\omega }^2$$

Solve for I, substitute:

$$I_{exD}=\frac{2K_{rot}}{w^2}$$ $$I_{exD}=\frac{2(m_{e}gd-0.5m_e\frac{4d^2}{t^2})}{{\frac{(\frac{2d}{t})}{r}}^2}$$ $$I_{exD}=\frac{2((0.05-0.0055)(9.81)(0.906)-0.5(0.05-0.0055)\frac{4(0.906{)}^2}{(22.33{)}^2})}{{\frac{(\frac{2(0.906)}{22.33})}{0.0082}}^2}$$ $$I_{exD}=0.009994kg{m}^2$$

$I_D$ and % difference Calculation

$$I_D=0.5m_d{r}_d^2$$ $$I_D=0.00886kg{m}^2$$ $$\Delta I=100\frac{|I_D-IexD|}{0.5(I_D+I_{exD})}$$

This is wrong.. but not really.

Because of the unknown grove in the disk, I don’t think the theoretical is “accepted”

$$\Delta I=100\frac{|0.008882842625-0.009994|}{0.5(0.008882842625+0.009994)}=11.77\%$$

Calculate $I_{exR}$ and % diff

We only need to reuse symbolic solution for $I_{exD}$, substituting instead the values from the disk+ring experiment, and then subtract $I_{exD}$ from the result.

$$I_{exR}=\Sigma I-ID$$ $$\Sigma I=\frac{2(m_{e}gd-0.5m_e\frac{4d^2}{t^2})}{{\frac{(\frac{2d}{t})}{r}}^2}$$ $$\Sigma I=\frac{2((0.1-0.0095)(9.81)(0.906)-0.5(0.1-0.0095)\frac{4(0.906{)}^2}{(18.43{)}^2})}{{\frac{(\frac{2(0.906)}{18.43})}{0.0082}}^2}$$ $$\Sigma I=0.0111kg{m}^2$$

Resub:

$$I_{exR}=0.0111-0.00886=0.00224kg{m}^2$$

Get percent diff:

$$\Delta I_R=100\frac{|I_R-IexR|}{0.5(I_R+I_{exR})}$$

Theoretical moment:

$$I_R=0.5m_R(r_{ri}^2+r_{ro}^2)$$ $$I_R=0.5(1.429)(0.0512^2+0.0635^2)=0.0047$$

Substitute:

$$\Delta I_R=100\frac{|0.0047-0.00224|}{0.5(0.0047+0.00224)}$$ $$=70.9\%$$

…eeesh but it’s a smaller proportion of $\Sigma I$, so maybe it’s reasonable.. I can’t find an error so I guess we roll with it.

Calculate $I_{exDV}$ and % Error

$$I_{exDV}=\frac{2(m_{e}gd-0.5m_e\frac{4d^2}{t^2})}{{\frac{(\frac{2d}{t})}{r}}^2}$$ $$I_{exDV}=\frac{2((0.05-0.0055)(9.81)(0.906)-0.5(0.05-0.0055)\frac{4(0.906{)}^2}{(16.46{)}^2})}{{\frac{(\frac{2(0.906)}{16.46})}{0.0082}}^2}$$ $$I_{exDV}=0.00399kg{m}^2$$

Calculate theoretical value (if it were perfectly flat):

$$I_{DV}=0.25m_d{r}_d^2$$ $$I_{DV}=0.25(1.426)(0.1115{)}^2=0.00443$$

Get percent error:

$$\Delta I_{DV}=100\frac{|0.00443-0.00399|}{0.5(0.00443+0.00399)}$$ $$\Delta I_{DV}=10.5\%$$

$I_A$ (Axle) Calculation

Find mass (using $cm$ bc I’m lazy):

$$m_A=\pi r^{2}h\rho$$ $$m_A=\pi (1.2{)}^2(18.2)(2.7)=0.222kg$$

Find $I_A$ (back in m):

$$I_A=0.5m{r}^2$$ $$I_A=0.5(0.222)(0.012{)}^2=0.000015kg{m}^2$$

Find % of flat disk system:

$$=100\frac{I_A}{IexD}=100\frac{0.000015}{0.009994}=0.15\%$$

This is an order of magnitude under the experimental-theoretical error, and so I deem it irrelevant.

Impact of axle on $I_{exR}$

The existence of the axle impacts the experimental measurement and calculation of the moment of the disk, $I_{exD}$. Since the moment of the ring, $I_{exR}$ is found by the difference of the moment of the system with and without the ring in place, the moment of the axle does not effect the values of $I_{exR}$.

Sources of error

Systematic

Air resistance:
Especially in the case of the vertically placed disk, air resistance will impact our results because it does not act constantly, and so cannot be accounted for by the friction mass.
Non-Constant Friction:
There is no reason to assume the particular scenario of friction in the ball bearings or bushings of the fixture remains constant with rotational velocity. If there is oil for example in the bearings, then the friction will in some part follow laws of hydrodynamics.
Reaction Time (Delay):
People are slow. The reaction time of a normal human is somewhere between 0.1 and 0.4 seconds depending on how much they slept, ate, etc. There is a positive delay between the driving mass contacting the floor and the experimenter stopping the time. Likewise, there is a delay between one experimenter starting the time and the other releasing the driving mass from it’s starting position.
Placement inaccuracy:
If the ring is placed off-center, there will be some radial load on the apparatus, which may cause it’s friction to behave strangely.

Random:

Reaction Time (inconsistency):
People are inconsistent. The reaction time of a human is different every time. There is a random time difference between the driving mass contacting the floor and the experimenter stopping the time. Likewise, there is a random time difference between one experimenter starting the time and the other releasing the driving mass from it’s starting position.
Measurement error:
In the measurement of the physical properties of the various elements of the apparatus, there is error. People aren’t that good at reading the meter stick.

Effects $I_D$: Air resistance, Non-Constant Friction, Reaction Time, Measurement Error
Effects $I_R$: Placement inaccuracy, Air resistance, Non-Constant Friction, Reaction Time, Measurement Error