Homework Problems

Backlog

A stone thrown upwards

Gravity: $A=-9.8m/s^2$
Initial Velocity: $V_0=8m/s$
Initial Position: $x_0=5$
(In Graph, X is time, Y is position)

y=-9.8x^2 + 8x + 5   

$$x=A{t}^2+V0+x_0$$ $$x=-9.8t^2+8t+5$$

Final time

$$\frac{-b+\text{sqr}It{b}^2-4ac}{2a}$$ $$\frac{-8+\sqrt{8^2-4(-9.8)5}}{2(-9.8)}$$ $$t_{final}=1.23084262738$$

Drone Descent

At 2m, -3m/s^2
Constant decel so x=0 when dx/dt = 0

y=-3x+2+(9/8)x^2  

Position Equation

$$x=-3t+2+\alpha t^2$$

Velocity equation

$$v=\partial x=-3t+2+\alpha t^2$$ $$v=-3+2\alpha t$$

Set both Position equation and velocity equation to zero because that’s what we care about, then solve for t.
Velocity:

$$t=\frac{3}{2\alpha }$$

Position:

$$t=\frac{3\pm \sqrt{9-8\alpha }}{2\alpha }$$

Solve as system to find A:

$$\frac{3}{2\alpha }=\frac{3\pm \sqrt{9-8\alpha }}{2\alpha }$$ $$3=3\pm \sqrt{9-8\alpha }$$ $$0=\sqrt{9-8\alpha }$$ $$0=9-8\alpha$$ $$\alpha =9/8$$

$\alpha$ is the coefficient responsible for acceleration in the equation for the drones position

But equation for position in terms of acceleration (derived from Constant acceleration eq 1) (with other factors removed) is:

$$x=\frac{1}{2}A{t}^2$$

Our equation (with other factors removed) is:

$$x=\frac{9}{8}\alpha t^2$$

So for $\alpha$ to equal $A$, we need to factor out the $1/2$ coefficient, resulting in:

$$x=\frac{1}{2}\frac{9}{4}{t}^2$$

Antelope Accelerating

$\Delta X$ = 65
$\Delta t$ = 7.8
$V_{t=7.8}$ = 15.9

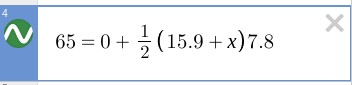
Diver at an Angle

V = 8 m/s & 30* above horizontal
Hits water 1.9s later
What was height of diving board
What angle did diver enter water

X axis

$V_0=4\sqrt{3}m/s^2$
$t=1.9s$
$a=-9.8m/s^2$
$x=0$

$$x=x_0+V_{0x}t-48.11$$ $$0=x_0+4\sqrt{3}\cdot 1.9-48.11$$ $$x_0=-4\sqrt{3}\cdot 1.9-48.11$$

__$x_0=34.9464138625$

Y axis

$V_0=4$
$t=1.9$
$a=0$
$Y_0=0$

$$Y_t=4\ast 1.9$$

$Y_t=7.6$

Combine

Car Ramp

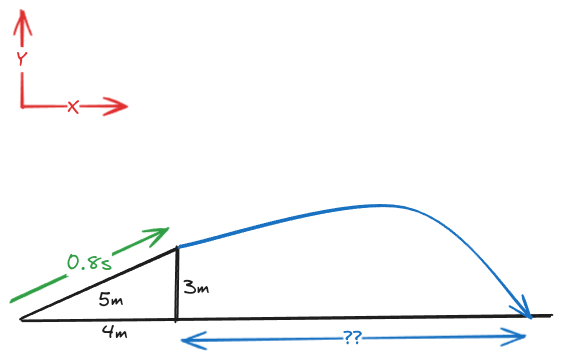
Length of Ramp

$X_0=0$
$X=5$
$V_0=0$
$t=0.8$

$$x=x_0+\frac{1}{2}(v_x+v_{0x})t$$ $$5=0+1/2(v_x+0)0.8$$

$V_x=12.5$

Angle = 36.87 degrees up from horizon

Y Axis (Up)

$$V_y=12.5\sin (36.87)$$

$V_y=7.5$
$A_y=-9.81m/s^2$
$Y_0=3$
$Y=0$

$$x=x_0+V_{0x}t+0.5A_x{t}^2$$ $$0=3+7.5t+0.5(-9.81)t^2$$

$t=1.8582$

X Axis (Right)

$$V_x=12.5cos(36.87)$$

$V_x=10$
$t=1.8582$

$$X=1.8582\cdot 10$$

$X=18.52$

Shooting water into tank

Spinning String or Hoop, axis aligned with gravity

$$T_y=G$$ $$T_x=C$$

Chapter 8 A

1 - Force of a baseball

A baseball has mass $m=0.142kg$ .

If the velocity of a pitched ball has a magnitude of $v=48.0m/s$and the batted ball’s velocity is $v=56.0m/s$ in the opposite direction, find the magnitude of the change in momentum of the ball and of the impulse applied to it by the bat.

momentum as a function of velocity from work and energy equations:

$$P=mv$$

Substitute to find initial momentum:

$$P_i=(0.142)(48)$$ $$P_i=6.816kgm/s$$

Substitute to find final momentum:

$$P_f=(0.142)(-56)$$ $$P_f=-7.952kgm/s$$

We can say that the change in momentum is equal to the difference in initial and final momentum

$$\Delta P=P_f-P_i$$ $$\Delta P=-14.768kgm/s$$ $$|\Delta P|=14.768kgm/s$$

If the ball remains in contact with the bat for $2.5ms$, find the magnitude of the average force applied by the bat.

Our $\Delta P$ is a unit of impulse, in $kgm/s$ or “newton-seconds”, $14kgm/s$ means 14 newtons applied for one second, so we can divide newton seconds by time to get netwons.

$$F=\Delta P/0.0025$$ $$F=5920N$$

2 - Space shuttle’s OMS

An engine of the orbital maneuvering system (OMS) on a space shuttle exerts a force of $2.63\times 10^{4}N$ over a time interval of $3.80s$ , exhausting a negligible mass of fuel relative to the shuttle’s mass of $9.53\times 10^4$

What is the shuttle’s change in momentum from this impulse?

We know from work and energy equations that impulse in newton seconds is:

$$J=Ft$$ $$J=2.63\times 10^4\cdot 3.8$$ $$J=99940$$

What is the shuttle’s change in velocity from this impulse?

We also know that change in momentum is equal to the magnitude of the impulse which did that change… from work and energy equations that change in momentum is:

$$\Delta P=m\Delta v$$

Reworking:

$$\Delta P/m=\Delta v$$

Substitute:

$$\frac{99940}{9.53\times 10^4}=\Delta V$$ $$\Delta V=1.05m/s$$

Why can’t we find the resulting change in the kinetic energy of the shuttle?

If you copy my answer verbatim....

We cannot find the resulting change in kinetic energy because kinetic energy relies on $v^2$, not just $v$, and so only knowing the $\Delta v$ is not enough, we would also need to know the starting or ending velocity.

3 - Rocket in outer space - varying force

At time $t=0$, a $2150kg$ rocket in outer space fires an engine that exerts an increasing force on it in the $+x$-direction. This force obeys the equation $F=A{t}^2$, where $1.45s$ is time, and has a magnitude of $781.25N$ when $t=1.45s$.

Find the SI value of the constant A.
Just solve the equation for A:

$$781=A(1.45{)}^2$$ $$A=371.46$$

What impulse does the engine exert on the rocket during the $1.50s$ interval starting $2.00s$ after the engine is fired?
Integrate force equation with respect to time over given interval:

$$J={\int }_{T_i}^{T_f}A{t}^{2}dt$$

Substitute:

$$J={\int }_2^{3.5}371.46t^{2}dt$$ $$J=\frac{371.46}{3}{t}^3{|}_2^{3.5}$$ $$J=4318.22$$

By how much does the rocket’s velocity change during this interval?
We know from the work and energy equations that Impulse (J) = change in momentum $\Delta P$ = $m\Delta v$, applying this:

$$J=m\Delta v$$ $$J/m=\Delta V$$

Substitute:

$$4318.22/2150=\Delta V$$ $$\Delta V=2m/s$$

4 - Very Strange Wall

A $2.50kg$ stone is sliding to the right on a frictionless horizontal surface at $6.00m/s$ when it is suddenly struck by an object that exerts a large horizontal force on it for a short period of time. The graph in the figure shows the magnitude of this force as a function of time.

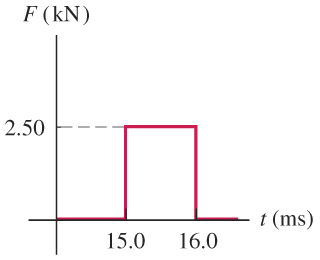
What impulse does this force exert on the stone?
We know from work and energy equations:

$$J=Ft$$

Substitute:

$$J=2.5kgm/s$$

Just after the force stops acting, find the magnitude of the stone’s velocity if the force acts to the right.
We can find the $\Delta v$ associated with the impulse with… work and energy equations:

$$P=m\Delta v$$ $$\Delta v=P/m$$

Substitute:

$$\Delta v=2.5/2.5$$ $$\Delta v=1$$ $$V_f=V_i+\Delta v$$ $$V_f=6+1=7m/s$$

5 - Funky box

Starting at $t=0s$ , a horizontal net force $\vec{F}=0.27t\hat{i}-4.6t^2\hat{j}$ is applied to a box that has an initial momentum $\vec{p}=-3.15\hat{i}+4.1\hat{j}$.

What is the momentum of the box at $t=2.15s$?

Solve for the x impulse using the work and energy equations:

$$J_x={\int }_0^{2.15}0.27tdt$$ $$J_x=0.624kgm/s$$

Solve for the y impulse using the work and energy equations:

$$J_y={\int }_0^{2.15}-0.46t^{2}dt$$ $$J_x=-1.52kgm/s$$

Add these to the initial momentum:
x:

$$P_{xf}=-3.15+0.624=-2.53kgm/s$$

y:

$$P_{yf}=4.1-1.52=2.6kgm/s$$

7 - Squids

Squids and octopuses propel themselves by expelling water. They do this by keeping water in a cavity and then suddenly contracting the cavity to force out the water through an opening. A $7.00kg$ squid (including the water in the cavity) at rest suddenly sees a dangerous predator.

If the squid has $1.75kg$ of water in its cavity, at what speed must it expel this water to instantaneously achieve a speed of $2.50m/s$ to escape the predator? Neglect any drag effects of the surrounding water.

Solve first for a needed impulse on the squid:

$$J_s=m\Delta v$$

The water would not accelerate with the squid…

$$J_s=(7-1.75)\ast 2.5=13.125kgm/s$$

Solve for velocity of water:

$$J_w=m\Delta v$$ $$J_w/m=\Delta v$$

Substitute:

$$13.125/1.75=\Delta v$$ $$\Delta v=7.5$$

How much kinetic energy does the squid create by this maneuver?

$$K=0.5m{v}^2$$

The total kinetic energy includes the moving squid and water it expelled..
Squid:

$$K_s=0.5\ast 5.25\ast 2.5^2$$ $$K_s=16.40625J$$

Water:

$$K_w=1.75\ast 7.5^2$$ $$K_w=49.21875J$$ $$\Sigma K=K_w+K_s$$ $$\Sigma K=65.6J$$

8 - Bumper Cars

When cars are equipped with flexible bumpers, they will bounce off each other during low-speed collisions, thus causing less damage. In one such accident, a $1850kg$ car traveling to the right at $1.50m/s$ collides with a $1350kg$ car going to the left at $1.10m/s$ . Measurements show that the heavier car’s speed just after the collision was $0.260m/$ in its original direction. You can ignore any road friction during the collision.

What was the speed of the lighter car just after the collision?
Solve for the impulse using the heavier car..

$$J=m\Delta v$$ $$J=1850(1.5-0.26)$$ $$J=2294kgm/s$$

Solve for $v_f$ of lighter car after impulse $J$ using $J=m\Delta v$:

$$J=1350\ast (1.1-v_f)$$

Here, positive is original direction… but question asks for speed, so we don’t even care.
**

$$v_f=-0.599m/s$$

Calculate the change in the combined kinetic energy of the two-car system during this collision.**
Heavy car:

$$\Delta K_h=0.5m{v}_f^2-0.5m{v}_i^2$$ $$\Delta K_h=0.5(1850)(0.26{)}^2-0.5(1850)(1.5{)}^2$$ $$\Delta K_h=-2018.72J$$

Light car:

$$\Delta K_l=0.5m{v}_f^2-0.5m{v}_i^2$$

Kinetic energy uses velocity magnitude: Speed... velocity shant be negative

$$\Delta K_l=0.5(1350)(0.599{)}^2-0.5(1350)(1.1{)}^2$$ $$\Delta K_l=-574.56J$$

Sum:

$$\Sigma \Delta K=\Delta K_h+\Delta k_l$$ $$\Sigma \Delta K=-2593.28J$$

Chapter 8 B

1 - Spring and two blocks

Block A in the figure has mass $1.00kg$, and block B has mass $3.00kg$. The blocks are forced together, compressing a spring S between them; then the system is released from rest on a level, frictionless surface. The spring, which has negligible mass, is not fastened to either block and drops to the surface after it has expanded. Block B acquires a speed of $1.10m/s$ .

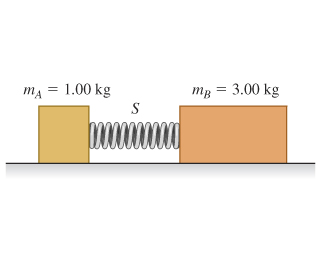
What is the final speed of block A?

Every action has an equal opposite reaction, so the force which accelerates block B will have the same magnitude and length, and thus impulse as it’s pair force which accelerates block A in the other direction.

Solve for momentum and thus impulse on block B using momentum formula from work and energy equations:

$$P=mv$$ $$P=3(1.1)$$ $$P=3.3kgm/s$$

Now solve for v of block A using the same forumla:

$$P=3.3=mv$$ $$3.3=1(v)$$ $$v_A=3.3m/s$$

How much potential energy was stored in the compressed spring?
Calculate and sum the potential energy for each block:
B:

$$K_B=0.5m{v}^2$$ $$K_B=0.5(3)(1.1{)}^2$$ $$K_B=1.815J$$

A:

$$K_A=0.5(1)(3.3{)}^2$$ $$K_A=5.445$$

Sum:

$$\Sigma K=K_A+K_B=7.26J$$

2 - Throwing a rock because you can’t ice skate

You are standing on a large sheet of frictionless ice and are holding a large rock. In order to get off the ice, you throw the rock so it has velocity relative to the earth of $11.9m/s$ at an angle of $36.0$ degrees above the horizontal.

If your mass is $73.0kg$ and the rock’s mass is $14.0kg$ , what is your speed after you throw the rock?

We know that the impulse on the rock and person must be the same, so we can solve for the impulse on the rock via it’s final momentum, since it’s initial velocity and thus momentum was zero.

Horizontal component of rock velocity:

$$v_R=11.8cos(36)=9.55$$ $$P_R=m_R{v}_R$$ $$P_R=14\ast 9.55$$ $$P_R=133.65kgm/s$$

Since their momentum’s are equal, we can solve for the velocity of the person:

$$P_P=m_P{v}_P$$ $$v_P=P_P/m_P$$ $$v_P=133.65/73$$ $$v_P=1.83m/s$$

3 - Canister in space

An astronaut in space cannot use a scale or balance to weigh objects because there is no gravity. But she does have devices to measure distance and time accurately. She knows her own mass is $76.4kg$, but she is unsure of the mass of a large gas canister in the airless rocket. When this canister is approaching her at $3.60m/s$ , she pushes against it, which slows it down to $1.30m/s$ (but does not reverse it) and gives her a speed of $2.60m/s$.

What is the mass of this canister?

The momentum of the canister will equal the momentum of the astronaut and canister at the end, so long as the astronaut is stopped before contacting the canister.

$$P_{Ci}=P_{Af}+P_{Cf}$$

Expand using momentum formula:

$$m_C{v}_{Ci}=m_A{v}_{Af}+m_C{v}_{Cf}$$ $$m_C(3.6)=(76.4)(2.6)+m_C(1.3)$$

Solve for $m_C$:

$$m_C=86.365kg$$

4 - Asteroid collision

Two asteroids of equal mass in the asteroid belt between Mars and Jupiter collide with a glancing blow. Asteroid A, which was initially traveling at $v_{A1}=40.0m/s$ with respect to an inertial frame in which asteroid B was at rest, is deflected $30.0$ degrees from its original direction, while asteroid B travels at $45.0$ degrees to the original direction of A, as shown in the figure.

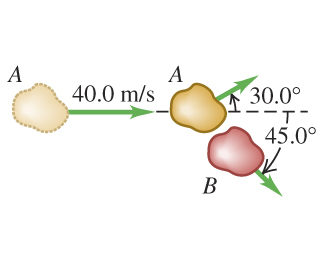
Find the speed of asteroid A after the collision.
Find the speed of asteroid B after the collision.

Conservation of momentum will apply in both the x and y directions:

$$\Sigma P_x=40m$$

m is the mass of either asteroid

$$\Sigma P_y=0$$

We can solve for their y velocities:

$$0=P_{Ay}+P_{By}$$ $$|P_{Ay}|=|P_{By}|$$ $$m{v}_{A}sin(30)=m{v}_{B}sin(45)$$ $$v_{A}sin(30)=v_{B}sin(45)$$

Solve for $v_A$:

$$v_A=\frac{v_{B}sin(45)}{sin(30)}$$

We can also express their x velocities:

$$\Sigma P_x=40m=P_{Ax}+P_{Bx}$$ $$\Sigma P_x=40m=m{v}_{A}cos(30)+m{v}_{B}cos(45)$$ $$\Sigma P_x/m=40=v_{A}cos(30)+v_{B}cos(45)$$

Substitute in $v_A$:

$$\Sigma P_x=40=\frac{v_{B}sin(45)}{sin(30)}cos(30)+v_{B}cos(45)$$ $$v_B=20.7m/s$$

Pull back up y momentum equation to find $v_A$:

$$v_{A}sin(30)=v_{B}sin(45)$$ $$v_{A}sin(30)=20.7sin(45)$$ $$v_A=\frac{20.7sin(45)}{sin(30)}$$ $$v_A=29.27$$

What fraction of the original kinetic energy of asteroid A dissipates during this collision?

# Given values  
v_A1 = 40.0  # initial velocity of asteroid A in m/s  
v_A2 = 29.3  # final velocity of asteroid A in m/s  
v_B2 = 20.7  # final velocity of asteroid B in m/s  
m = 1  # mass of the asteroids (we'll keep it as 1 for simplicity since it cancels out)  
  
# Initial kinetic energy of asteroid A  
KE_A_initial = 0.5 * m * v_A1**2  
  
# Final kinetic energies of asteroids A and B  
KE_A_final = 0.5 * m * v_A2**2  
KE_B_final = 0.5 * m * v_B2**2  
  
# Total initial and final kinetic energies  
KE_initial = KE_A_initial  
KE_final = KE_A_final + KE_B_final  
  
# Fraction of the kinetic energy dissipated  
fraction_dissipated = (KE_initial - KE_final) / KE_initial  
print(fraction_dissipated)  

$$=0.196$$

6 - Bullet into wood

A bullet of mass $6.00g$ is fired horizontally into a wooden block of mass $1.29kg$ resting on a horizontal surface. The coefficient of kinetic friction between block and surface is ${\mu }_k=0.220$ The bullet remains embedded in the block, which is observed to slide a distance $0.210m$ along the surface before stopping.

What was the initial speed of the bullet?
We can first find the initial velocity of the block using kinematics equations:

$$V_x^2=V_{0x}^2+2A_x(x-x_0)$$ $$0=V_{0x}^2+2A_x(0.21)$$

We need to find the acceleration:

$$F_{net}=ma$$ $$a=F/m$$

We know that F is the product of ${\mu }_k$, $m$, and $g$

$$a=\frac{{\mu }_{k}mg}{m}$$ $$a={\mu }_{k}g$$

Plugging back into kinematics:

$$0=V_{0x}^2+2{\mu }_{k}g(0.21)$$ $$V_{0x}^2=-2{\mu }_{k}g(0.21)$$ $$V_{0x}=\sqrt{-2{\mu }_{k}g(0.21)}$$ $$-V_{0x}=\sqrt{2(0.22)(9.81)(0.21)}$$ $$V_0=0.95m/s$$

Now we solve for the impulse needed to get the wood to that speed using work and energy equations:

$$J=m\Delta V$$ $$J=1.29(0.95)$$ $$J=1.2255kgm/s$$

Now we solve for the momentum of the bullet required for that impulse:

$$P=mv$$ $$1.2255=0.006v$$ $$v=1.2255/0.006$$ $$v=204.25m/s$$

7 - Ballistic pendulum

In a ballistic pendulum an object of mass $m$ is fired with an initial speed $v_0$ at a pendulum bob. The bob has a mass $M$, which is suspended by a rod of length $L$ and negligible mass. After the collision, the pendulum and object stick together and swing to a maximum angular displacement $\theta$ as shown.

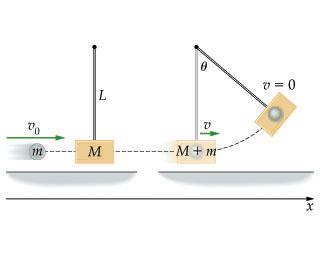
Find an expression for $v_0$, the initial speed of the fired object.
Express your answer in terms of some or all of the variables $m$, $M$, $L$, and $\theta$ and the acceleration due to gravity, $g$.

Game plan:

1. Get $\Delta U$ between top and bottom of pendulum swing
2. Knowing that $K$ at the bottom (right after collision) of the pendulum equals $\Delta U$, solve for initial velocity of pendulum
3. Find impulse needed to create momentum with initial velocity of pendulum
4. Find velocity of mass $m$ so that it’s momentum is equal to impulse needed

1: From work and energy equations:

$$\Delta U=mgh$$ $$\Delta U=(m+M)g(L-Lcos(\theta ))$$

2: From work and energy equations:

$$K=0.5m{v}^2$$ $$K=0.5(m+M)v^2$$ $$v=\sqrt{\frac{2K}{m+M}}$$

Substitute:

$$v=\sqrt{\frac{2(m+M)g(L-Lcos(\theta ))}{m+M}}$$ $$v=\sqrt{2g(L-Lcos(\theta ))}$$

3: From work and energy equations:

$$J=m\Delta v$$ $$J=(m+M)\sqrt{2g(L-Lcos(\theta ))}$$

4: From work and energy equations:

$$J=m\Delta v$$ $$(m+M)\sqrt{2g(L-Lcos(\theta ))}=mv$$ $$v=\frac{(m+M)\sqrt{2g(L-Lcos(\theta ))}}{m}$$

An experiment is done to compare the initial speed of bullets fired from different handguns: a $9.0mm$ and a $.44$ caliber. The guns are fired into a $10kg$ pendulum bob of length $L$. Assume that the $9.0mm$ bullet has a mass of $6.0g$ and the $.44$ caliber bullet has a mass of $12g$. If the $9.0mm$ bullet causes the pendulum to swing to a maximum angular displacement of $4.3^{\circ }$ and the $.44$ caliber bullet causes a displacement of $10.1^{\circ }$ , find the ratio of the initial speed of the $9.0mm$ bullet to the speed of the $.44$ caliber bullet, $(v0)9.0/(v0)44$.

Just like ratio and simplify

$$\frac{\frac{(m+M)\sqrt{2g(L-Lcos(\theta ))}}{m}}{\frac{(m+M)\sqrt{2g(L-Lcos(\theta ))}}{m}}$$ $$\frac{\frac{(0.006+10)\sqrt{2g(L-Lcos(4.3))}}{0.006}}{\frac{(0.012+10)\sqrt{2g(L-Lcos(10.1))}}{0.012}}$$ $$\frac{(0.006+10)\sqrt{2g(L-Lcos(4.3))}}{(0.012+10)\sqrt{2g(L-Lcos(10.1))}}$$ $$=whothefuckknowsbuti{t}^{\prime }swrong$$

8 - Rebounding block and spring

A $15.0kg$ block is attached to a very light horizontal spring of force constant $525N/m$ and is resting on a smooth horizontal table. (See the figure below) Suddenly it is struck by a $3.00kg$ stone traveling horizontally at $8.00m/s$ to the right, whereupon the stone rebounds at $2.00m/s$ horizontally to the left.

Find the maximum distance that the block will compress the spring after the collision.

First find impulse done on the ball:

$$\Delta v_B=(2+8)$$

From the work and energy equations:

$$J=m\Delta v$$ $$J=3(10)$$ $$J=30$$

Now find velocity of block immediately after impact:

$$P=mv$$ $$30=15v$$ $$v=2m/s$$

Now find kinetic energy of the block after impact:

$$K=0.5m{v}^2$$ $$K=0.5(30)(2{)}^2$$ $$K=30J$$

Using known law: potential energy of spring = $U=0.5k{x}^2$

$$30=0.5(525)x^2$$ $$x=0.338m$$

9 - Protons elastically collide

You are at the controls of a particle accelerator, sending a beam of $4.20\ast 10^{7}m/s$ protons (mass $m$) at a gas target of an unknown element. Your detector tells you that some protons bounce straight back after a collision with one of the nuclei of the unknown element. All such protons rebound with a speed of $3.90\ast 10^{7}m/s$. Assume that the initial speed of the target nucleus is negligible and the collision is elastic.

Find the mass of one nucleus of the unknown element. Express your answer in terms of the proton mass

Kinetic energies:

$$\Delta K_P=0.5m(4.2\ast 10^7{)}^2-0.5m(3.9\ast 10^7{)}^2$$ $$\Delta K_p=0.5M{v}^2$$

So:

$$0.5m(4.2\ast 10^7{)}^2-0.5m(3.9\ast 10^7{)}^2=0.5M{v}^2$$ $$0.5m(4.2\ast 10^7)-0.5m(3.9\ast 10^7)=0.5Mv$$ $$\frac{m(4.2\ast 10^7)-m(3.9\ast 10^7)}{M}=v$$

Momentum:

$$J=m(4.2\ast 10^7)+m(3.9\ast 10^7)$$ $$J=Mv$$

So:

$$m(4.2\ast 10^7)+m(3.9\ast 10^7)=Mv$$

Combine:

$$\frac{m(4.2\ast 10^7)+m(3.9\ast 10^7)}{(\frac{m(4.2\ast 10^7)-m(3.9\ast 10^7)}{M})}=M$$

$$M=27m$$

Plug back in to find v:

$$\frac{m(4.2\ast 10^7)+m(3.9\ast 10^7)}{27m}=v$$ $$\frac{(4.2\ast 10^7)+(3.9\ast 10^7)}{27}=v$$ $$v=3\ast 10^6$$

10 - Cursed Billiards

Spheres A (mass $0.020kg$), B (mass $.030kg$), and C (mass $0.050kg$), are each approaching the origin as they slide on a frictionless air table (Figure 1). The initial velocities of A and B are $1.50m/s$ and $0.50m/s$. All three spheres arrive at the origin at the same time and stick together.

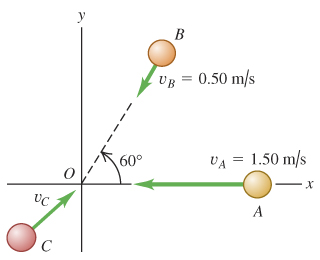
What must the x-component of the initial velocity of C be if all three objects are to end up moving at $0.50m/s$ in the +x-direction after the collision?

Vector momentums:

$$\overrightarrow{\Sigma P}=0.5\vec{i}$$

x:

$$-1.5(0.02)-0.5cos(60)(0.03)+C_x(0.05)=0.5(0.02+0.03+0.05)$$ $$c_x=1.75m/s$$

What must the y-component of the initial velocity of C be if all three objects are to end up moving at $0.50m/s$ in the $+x$-direction after the collision?
y:

$$-0.5sin(60)(0.03)+C_y(0.05)=0$$ $$C_y=0.26m/s$$

11 - Bullet, block and spring

A rifle bullet with mass $8.00g$ strikes and embeds itself in a block with mass $0.992kg$ that rests on a frictionless, horizontal surface and is attached to a coil spring. The impact compresses the spring $15.0cm$. Calibration of the spring shows that a force of $0.750N$ is required to compress the spring $0.250cm$

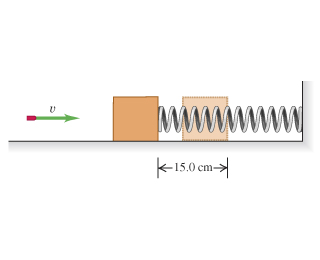
Find the magnitude of the block’s velocity just after impact.
Find spring constant:

$$F=kx$$ $$0.75=k(0.0025)$$ $$k=300N/m$$

Find potential energy change by compressing spring:

$$U_S=0.5k{x}^2$$ $$U_S=0.5(300)0.15^2$$ $$U_S=3.375J$$

Since kinetic energy at the start of the springs compression will equal the compressed potential energy difference, we need to calculate speed needed for the block to have that K:

$$K=0.5m{v}^2$$ $$v=\sqrt{\frac{2K}{m}}$$ $$v=\sqrt{2(3.375)/0.992}$$ $$v=2.61m/s$$

What was the initial speed of the bullet?

Sticky collision, so convert block + bullet momentum at v to bullet momentum and then to bullet velocity:

$$v_B=\frac{2.61(0.992+0.008)}{0.008}$$ $$v_B=326.25m/s$$

12 - Block lands in rolling car and…?

In a shipping company distribution center, an open cart of mass $49.0kg$ is rolling to the left at a speed of $5.20m/s$. You can ignore friction between the cart and the floor. A $13.0kg$ package slides down a chute that is inclined at $37$ degrees from the horizontal and leaves the end of the chute with a speed of $2.80m/s$ . The package lands in the cart and they roll off together.

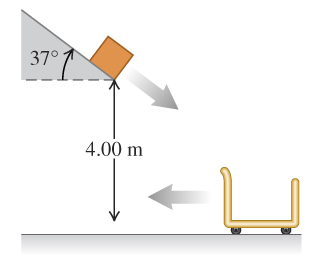
If the lower end of the chute is a vertical distance of $4.00m$ above the bottom of the cart, what is the speed of the package just before it lands in the cart?

Velocity as block leaves ramp:

$$v_{BXI}=cos(37)2.8=2.236m/s$$ $$v_{BYI}=sin(37)2.8=1.685m/s$$

Y velocity at bottom including gravity:

$$v_{BYF}=\sqrt{1.685^2+2(9.81)(4)}$$ $$v_{BYF}=9.02m/s$$

Total speed at impact:

$$v_{BF}=\sqrt{9.02^2+2.236^2}$$ $$v_{BF}=9.293m/s$$

What is the final speed of the cart?
Momentum of the cart (+x to the right):

$$P_C=-5.2(49)=-254.8kgm/s$$

Momentum of box in X:

$$P_{BX}=2.236(13)=29.068kgm/s$$

Final Velocity:

$$v_f=\frac{29.068-254.8}{13+49}=3.64m/s$$

Ch 08 Part C and 09 Part A

2 - Blocks of Chocolate

Three odd-shaped blocks of chocolate have the following masses and center-of-mass coordinates: $0.300kg$, $(0.210m,0.310m)$; $0.390kg$, $(0.110m,-0.400m)$; $0.210kg$ , $(-0.280m,0.620m)$.

Find the x-coordinate of the center of mass of the system of three chocolate blocks.
From Motion of Bodies in Free Space Equations:

$$\overrightarrow{r_c}=\frac{\Sigma \vec{p}m}{\Sigma m}$$ $$r_x=\frac{\Sigma xm}{\Sigma m}$$ $$r_x=\frac{0.3(0.21)+0.39(0.11)+0.21(-0.28)}{0.3+0.39+0.21}=0.052m$$

Find the y-coordinate of the center of mass of the system of three chocolate blocks.

$$r_y=\frac{\Sigma ym}{\Sigma m}$$ $$r_y=\frac{0.3(0.31)+0.39(-0.4)+0.21(0.62)}{0.3+0.39+0.21}=0.074m$$

3 - Particles

At one instant, the center of mass of a system of two particles is located on the x-axis at $x=2.0m$ and has a velocity of $(5.0m/s)\hat{i}$. One of the particles is at the origin. The other particle has a mass of $0.10kg$ and is at rest on the x-axis at $x=8.0m$.

What is the mass of the particle at the origin?
From Motion of Bodies in Free Space Equations:

$$r_c=r\frac{m_2}{m_1+m_2}$$ $$2=8\frac{0.1}{m_1+0.1}$$ $$2(m_1+0.1)=8(0.1)$$ $$m_1=\frac{8(0.1)-0.2}{2}=0.3$$

Calculate the total momentum of this system.
We know that the total momentum is the total mass multiplied by the velocity of the center of mass:

$$\Sigma P=V_c\Sigma m$$ $$\Sigma P=5(m_1+m_2)$$ $$\Sigma P=5\ast (0.3+0.1)=0.4\ast 5=2kgm/s$$

What is the velocity of the particle at the origin?
Since the particle not at the origin is not moving, the other particle must be moving rapidly enough to have all of the momentum of the system.

$$V_1{m}_1=2$$ $$V_1=\frac{2}{m_1}=\frac{2}{0.3}=6.66m/s$$

4 - Solar System

Find the position of the center of mass of the system of the sun and Jupiter.

$$m_s=1.989\times 10^{30}kg$$ $$m_j=1.898\times 10^{27}kg$$ $$r=778\ast 10^{9}m$$ $$r_c=r\frac{m_2}{m_1+m_2}$$ $$r_c=778\ast 10^9\frac{1.898\ast 10^{27}}{1.898\ast 10^{27}+1.989\ast 10^{30}}=741697465.164m$$

5 - Relative motion of a canoo and woman

A $45.0kg$ woman stands up in a $60.0kg$ canoe $5.00m$ long. She walks from a point $1.00m$ from one end to a point $1.00m$ from the other end.

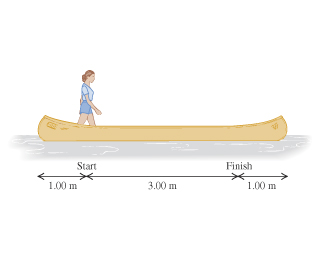
If you ignore resistance to motion of the canoe in the water, how far does the canoe move during this process?
In a closed system, the momentum of the center of mass must remain the same, if the momentum of the center of mass is zero in our frame of reference, it must remain zero. We need to find the movement of the canoo to counteract the movement of the person and keep the center of mass the same.

Initially the canoe’s center is at 0, and the woman’s center is at -1.5, and afterwards the canoe is at x, and she’s at x+1.5. The center of mass doesn’t change, so

$$\frac{45\ast -1.5+0\ast 60}{45+60}=\frac{45\ast (x+1.5)+x\ast 60}{45+60}$$ $$x=-9/7$$

6 - Rotating and Translating dumbell

This problem illustrates the two contributions to the kinetic energy of an extended object: rotational kinetic energy and translational kinetic energy. You are to find the total kinetic energy $K_{total}$ of a dumbbell of mass mm when it is rotating with angular speed $\omega$ and its center of mass is moving translationally with speed $v$. Denote the dumbbell’s moment of inertia about its center of mass by $I_{cm}$.

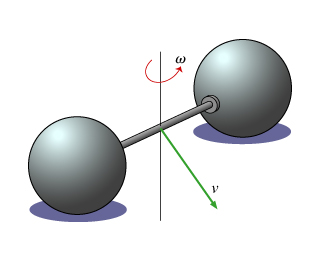
Find the total kinetic energy $K_{tot}$ of the dumbbell.
Just sum equations for linear and rotational kinetic energy from the work and energy equations:

$$k_{tot}=0.5I_{cm}{\omega }^2+0.5m{v}^2$$

9 - Motor shaft

At $t=0$ the current to a dc electric motor is reversed, resulting in an angular displacement of the motor shaft given by $\theta (t)=243t-19.9t^2-1.49t^3$.

At what time is the angular velocity of the motor shaft zero?
It is zero when:

$$\frac{d}{dt}\theta (t)=0$$ $$t=\frac{10\sqrt{148222}-1990}{447}$$ $$t=4.16$$

Calculate the angular acceleration at the instant that the motor shaft has zero angular velocity.
Second derivative:

$$-\frac{447t}{50}-\frac{199}{5}$$

19 - ??

20 - Spinning Earth

What is the moment of inertia of the Earth?
Use the uniform-sphere approximation described in the introduction. The mass of the Earth is 5.97×10^24kg, the radius of the Earth is 6.38×10^6mm, and the period of rotation for the Earth is 24.0hours. The moment of inertia of a uniform sphere is given by the equation:

I=\frac{2}{5}MR^2 $$ We can plug in the given values to find I:

I=\frac{2}{5}(5.97\cdot10^{24})(6.38\cdot10^6)= 9.72×10^{37} kg⋅m

$$\ast \ast WhatistherotationalkineticenergyoftheEarth?\ast \ast UsethemomentofinertiayoucalculatedinPartAratherthantheactualmomentofinertiagiveninPartB.Rotationalkineticenergyisgivenbytheequation:$$

KE_{rot}=\frac{1}{2} I \omega

$$However,wefirsthavetosolvefortheangularspeed(omega).$$

\omega = \frac{2\pi}{T}

T=24 \cdot 3600 =86400

\omega =\frac{2\pi}{86400} = 7.27\cdot10^{-5} $$ Going back to the original formula, we can now find $K{E}_{rot}$.

$$K{E}_{rot}=\frac{1}{2}I{\omega }^2=\frac{1}{2}(9.72\cdot 10^{37})(7.27\cdot 10^{-5}{)}^2=2.57\cdot 10^{29}J$$

Chapter 9 Part B

1 - Pulley

A frictionless pulley has the shape of a uniform solid disk of mass $2.80kg$ and radius $10cm$. A $1.90kg$ stone is attached to a very light wire that is wrapped around the rim of the pulley, and the system is released from rest.

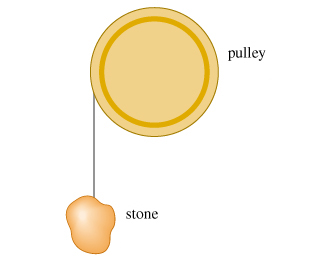
How far must the stone fall so that the pulley has $7.00J$ of kinetic energy?

The energy of the full system can be written as:

$$Fd=\frac{1}{2}I{\omega }^2+0.5m{v}^2$$

and:

$$\omega =\frac{v}{r}$$

So…

$$Fd=\frac{1}{2}I{\frac{v_s}{r}}^2+0.5m_s{v}_s^2$$

A disks mass moment of intertia:

$$I=0.5m{r}^2$$

Combining these two:

$$Fd=\frac{1}{4}(m_p{r}^2){\frac{v_s}{r}}^2+0.5m_s{v}_s^2$$

We are told that the kinetic energy of the pulley is $K_p$ or $7J$ (I separated out the first term from above, which is the kinetic energy of the pulley in terms of the velocity of the stone):

$$\frac{1}{4}{m}_p{v}_s^2=K_p$$ $$v_s^2=\frac{4K_p}{m_p}$$

Recombine:

$$Fd=K_p+0.5m_s\frac{4K_p}{m_p}$$ $$d=\frac{K_p+0.5m_s\frac{4K_p}{m_p}}{m_{s}g}$$

Substituting problem values:

$$d=\frac{7+0.5(1.9)\frac{4(7)}{2.8}}{1.9(9.81)}$$ $$d=0.88m$$

What percent of the total kinetic energy does the pulley have?
Total kinetic energy:

$$\Sigma K=m_{s}gd$$ $$\frac{K_p}{\Sigma K}=\frac{K_p}{m_{s}gd}$$

7 - Pulley and blocks

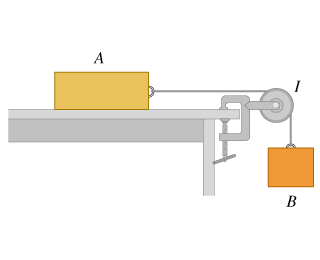
Use energy methods to calculate the speed of block B as a function of the distance d that it has descended.
Express your answer in terms of the variables $m_A$, $m_B$, $R$, $I$, ${\mu }_k$, $d$ and appropriate constants.

Net force:

$$F=m_{B}g-m_A{\mu }_{k}g$$

Net work:

$$W=(m_{B}g-m_A{\mu }_{k}g)d$$

Kinetic energy:

$$\Sigma K=W=(m_{B}g-m_A{\mu }_{k}g)d=0.5(m_A+m_B)v^2+0.5I{\frac{v}{r}}^2$$

Solve for v:

$$2(m_{B}g-m_A{\mu }_{k}g)d=(m_A+m_B)v^2+I\frac{v^2}{r^2}$$ $$2(m_{B}g-m_A{\mu }_{k}g)d=(m_A+m_B)v^2+I\frac{v^2}{r^2}$$ $$2(m_{B}g-m_A{\mu }_{k}g)d=((m_A+m_B)+I\frac{1}{r^2})(v^2)$$ $$\frac{2(m_{B}g-m_A{\mu }_{k}g)d}{((m_A+m_B)+I\frac{1}{r^2})}=(v^2)$$ $$\sqrt{\frac{2(m_{B}g-m_A{\mu }_{k}g)d}{((m_A+m_B)+I\frac{1}{r^2})}}=v$$

8 - Block, Pulley, Gravity

The pulley in the figure has radius $0.160m$ and a moment of inertia $0.560kg\cdot m^2$. The rope does not slip on the pulley rim.

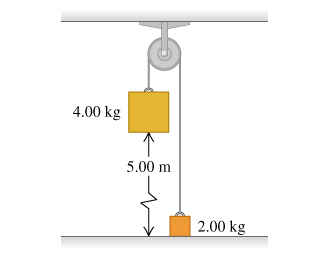Use energy methods to calculate the speed of the 4.00-kg block just before it strikes the floor.

Just use the equation from question 7 but delete friction:

$$\sqrt{\frac{2(m_{B}g-m_{A}g)d}{((m_A+m_B)+I\frac{1}{r^2})}}=v$$ $$v=2.653$$

Two Discs

Two metal disks, one with radius $R_1=2.60cm$ and mass $M_1=0.800kg$ and the other with radius $R_2=4.90cm$ and mass $M_2=1.70kg$, are welded together and mounted on a frictionless axis through their common center.
Find moments of intertia:

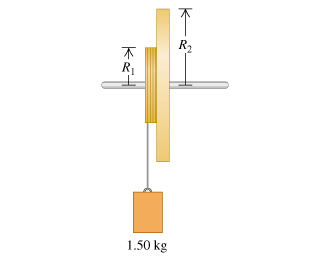What is the total moment of inertia of the two disks?

$$I=0.5m{r}^2$$ $$I_1=0.5(0.8)(0.026{)}^2$$ $$I_2=0.5(1.7)(0.049{)}^2$$ $$I=0.5(0.8)(0.026{)}^2+0.5(1.7)(0.049{)}^2$$

A light string is wrapped around the edge of the smaller disk, and a 1.50-kg block, suspended from the free end of the string. If the block is released from rest at a distance of 1.95 m above the floor, what is its speed just before it strikes the floor?

$$fd=K_b+K_d$$ $$m_{B}gd=0.5m_B{v}^2+0.5I\frac{v^2}{r^2}$$ $$2m_{B}gd=(m_B+I\frac{1}{r^2})v^2$$ $$\sqrt{\frac{2m_{B}gd}{m_B+I\frac{1}{r^2}}}=v$$ $$v=3.41m/s$$

Chapter 10 A

7 - Book and Book and Pulley

A textbook of mass $1.93kg$ rests on a frictionless, horizontal surface. A cord attached to the book passes over a pulley whose diameter is $0.170m$ , to a hanging book with mass $2.96kg$. The system is released from rest, and the books are observed to move a distance $1.22m$ over a time interval of $0.780s$.

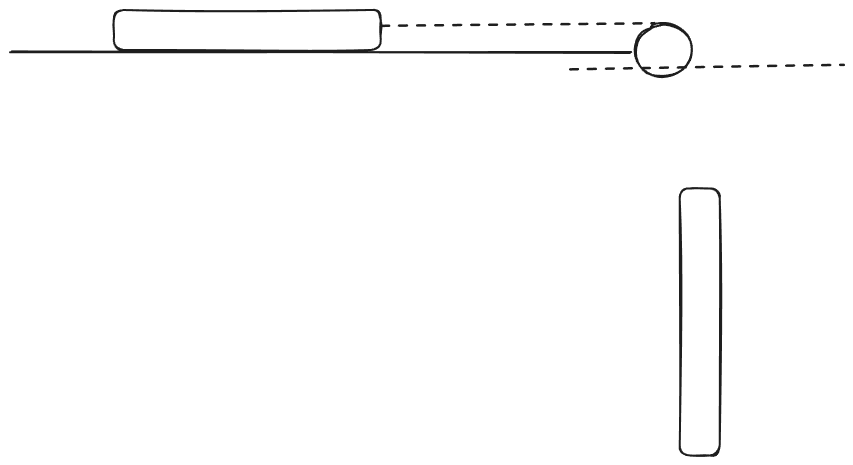
What is the tension in the part of the cord attached to the textbook?

$$\Sigma F=ma$$ $$T=ma$$

We need to find acceleration:

d=0.5A_xt^2 $$$$ \frac{2d}{t^2}=a

Substitute a back in:

$$T_1=m_1\frac{2d}{t^2}$$

What is the tension in the part of the cord attached to the book?
Solve for the tension by subtracting actual acceleration from acceleration due to gravity..

$$T_2=ma$$ $$T_2=m_2(9.8-\frac{2d}{t^2})$$

What is the moment of inertia of the pulley about its rotation axis?
The difference between $T_1$ and $T_2$ will tell us how much force is being used to accelerate the pulley. We can multiply that force by the pulley’s radius to find the torque acting on the pulley.

$$T=(T_2-T_1)r$$

We also know that net torque is equal to the product of moment of inertia and angular acceleration:

$$T=I\alpha$$

We need to find angular acceleration of the pulley:

$$\alpha =\frac{a}{r}$$

Substitute $\alpha$ equation into net torque equation and combine with known torque equation:

$$(T_2-T_1)r=I\frac{(\frac{2d}{t^2})}{r}$$

Solve for I:

$$\frac{(T_2-T_1)r}{\frac{(\frac{2d}{t^2})}{r}}=I$$

Desmos

8 - Frictionless Cube Vs. Rolling Cylinder

Two objects slide down two identical slopes, one is a circle and must roll to progress, while the other is a cube and has no friction when sliding down the slopes. They have identical masses.

What is the difference in arrival time at the end of the slope in terms of h, m, theta, and R as needed.

Length in terms of height and angle:

$$L=\frac{h}{sin(\theta )}$$

Decent time of cube:
(From first kinematic eq)

$$t=\sqrt{\frac{x}{0.5a}}$$ $$t=\sqrt{\frac{\frac{h}{sin(\theta )}}{0.5a}}$$

Find a:

$$F=ma$$ $$a=F/m$$ $$a=\frac{mgcos(\theta )}{m}$$ $$a=gcos(\theta )$$

Resub:

$$t_c=\sqrt{\frac{\frac{h}{sin(\theta )}}{0.5gcos(\theta )}}$$

Decent time of Disk:
Since acceleration is linear, find the final rotational and linear velocities using energy method, then use those to find average linear velocity

$$\Sigma K=FD=mgcos(\theta )L=K_L+K_R$$ $$mgcos(\theta )L=K_L+K_R$$

Find $K_R$ in terms of $K_L$:

$$K_L=0.5m{v}^2$$ $$K_R=\frac{1}{2}I{\omega }^2$$ $$K_R=\frac{1}{4}m{R}^2{\omega }^2$$ $$\omega =V/R$$ $$K_R=\frac{1}{4}m{R}^2\frac{v^2}{R^2}$$ $$K_R=\frac{1}{4}m{v}^2$$ $$mgcos(\theta )L=0.5m{v}^2+\frac{1}{4}m{v}^2$$

Solve for v:

$$mgcos(\theta )L=(0.5m+\frac{1}{4}m)v^2$$ $$\frac{mgcos(\theta )L}{(0.5m+\frac{1}{4}m)}=v^2$$ $$v=\sqrt{\frac{mgcos(\theta )L}{(0.5m+\frac{1}{4}m)}}$$

Use v to solve for t using 4st kinematic eq:

$$x=x_0+\frac{1}{2}(v_x+v_{0x})t$$ $$L=\frac{1}{2}\sqrt{\frac{mgcos(\theta )L}{(0.5m+\frac{1}{4}m)}}t$$ $$\frac{L}{\frac{1}{2}\sqrt{\frac{mgcos(\theta )L}{(0.5m+\frac{1}{4}m)}}}=t$$ $$\frac{\frac{h}{sin(\theta )}}{\frac{1}{2}\sqrt{\frac{mgcos(\theta )\frac{h}{sin(\theta )}}{(0.5m+\frac{1}{4}m)}}}=t$$

Not sure why I shat the bed.. but

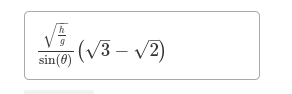
9 - easier version of 8 kms

https://chatgpt.com/share/6720011b-87d8-8002-9055-3f35b60303db

Chapter 10 B

Item 8

Chapter 11 A

1 - Block, String, String

A rigid, uniform, horizontal bar of mass $m_1$ and length $L$ is supported by two identical massless strings. Both strings are vertical. String A is attached at a distance $d<L/2$ from the left end of the bar and is connected to the ceiling; string B is attached to the left end of the bar and is connected to the floor. A small block of mass $m_2$ is supported against gravity by the bar at a distance $x$ from the left end of the bar, as shown in the figure.
Throughout this problem positive torque is that which spins an object counterclockwise.

Find $T_A$, the tension in string A.
Equilibrium Conditions about left end:

$$\Sigma F=0=T_A-T_B-(m_1+m_2)g$$ $$T_B=T_A-(m_1+m_2)g$$

You could isolate $T_A$ from the top force equation, but it’s easier to just use the torque equation.

$$\Sigma \tau =0=T_{A}d-m_{1}g(0.5L)-m_{2}gx$$ $$T_A=\frac{m_{1}g(0.5L)+m_{2}gx}{d}$$

Find $T_B$, the magnitude of the tension in string $B$.

$$\Sigma F=0=T_A-T_B-(m_1+m_2)g$$ $$T_B=T_A-(m_1+m_2)g$$

If the mass of the block is too large and the block is too close to the left end of the bar (near string $B$) then the horizontal bar may become unstable (i.e., the bar may no longer remain horizontal).
What is the smallest possible value of $x$ such that the bar remains stable (call it $x_{critical}$)?
The tension in string B needs to be greater than zero for the system to be in equilibrium, because strings don’t have compressive strength. We need to find the x value where $T_A=0$
Torque about point where A attaches to bar (keep in mind that $m_1$ is now on the left side of the axis of rotation):

$$\Sigma {\tau }_A=T_B-(d-0.5L)m_{1}g+(x-d)m_{2}g$$ $$0=-(d-0.5L)m_{1}g+(x-d)m_{2}g$$ $$(d-0.5L)m_{1}g=(x-d)m_{2}g$$ $$\frac{(d-0.5L)m_{1}g}{m_{2}g}+d=x$$

Note that $x_{critical}$, as computed in the previous part, is not necessarily positive. If $x_{critical}<0$, the bar will be stable no matter where the block of mass $m2$ is placed on it.

Assuming that $m1$, $d$, and $L$ are held fixed, what is the maximum block mass $m_{max}$ for which the bar will always be stable? In other words, what is the maximum block mass such that $x_{critical}\le 0$?

$$\frac{(0.5L-d)m_{1}g}{m_{2}g}+d=0$$ $$\frac{(0.5L-d)m_{1}g}{m_{2}g}=d$$ $$(0.5L-d)m_{1}g=dg{m}_2$$ $$\frac{(0.5L-d)m_{1}g}{dg}=m_2$$

2 - Hanging shelf

(-nalini)
()

4 - Boy on beam

A uniform, aluminum beam 9.00 m long, weighting 300 N, rests symmetrically on two supports 5.00 m apart. A boy weighing 600 N starts at point A and walks toward the right.

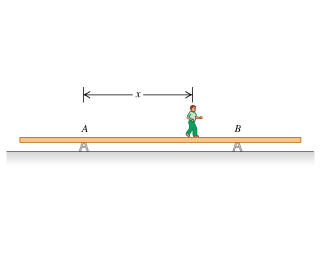
How far beyond point B can the boy walk before the beam tips?
The center of gravity will be at B when it is about to tip. In this case, center of mass is the same formula as center of mass.

$$r_c=r\frac{m_2}{m_1+m_2}$$ $$2.5=r\frac{600}{300+600}$$ $$r=\frac{2.5}{\frac{600}{300+600}}=3.75$$ $$3.75-2.5=1.25$$

How far from the right end of the beam should support B be placed so that the boy can walk just to the end of the beam without causing it to tip?
solve for center of mass with child as $m_1$ and center of beam being 4.5m away

$$r_c=4.5\frac{1}{3}=1.5$$

5 - What the $\theta$

In each case let w be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w.

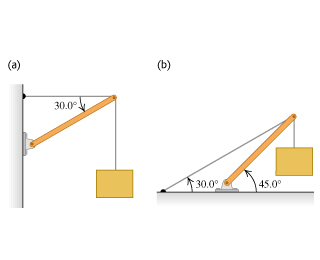
Find the tension $T$ in the cable in the arrangement (a).
Harvard phd student did it :)
Harvard phd student also thinks the question and answer are wrong. Something about how the pulley don’t make sense…

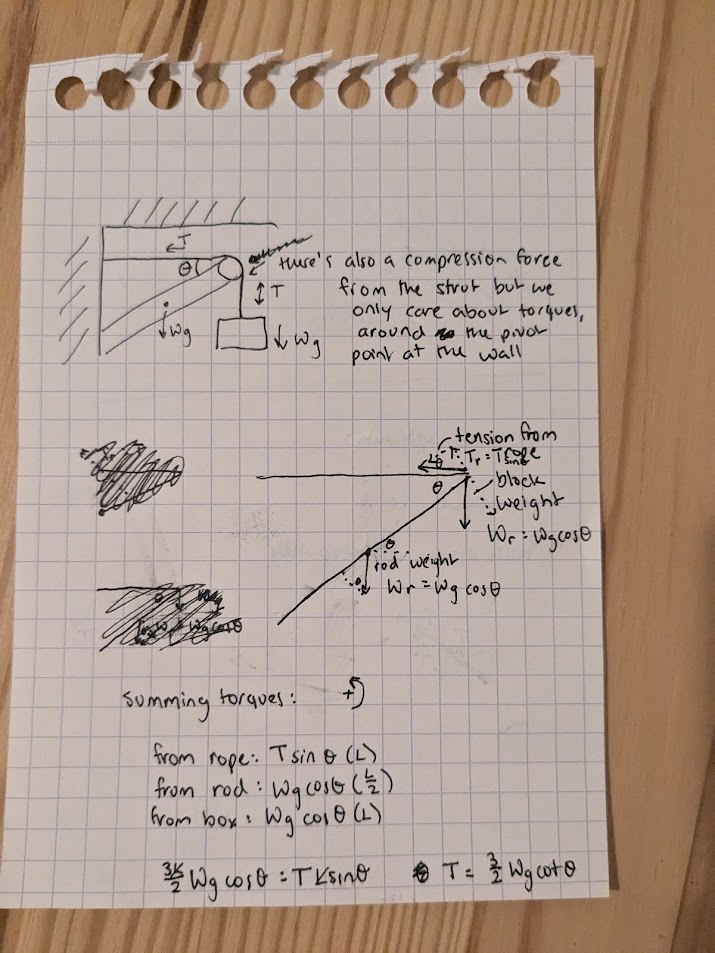
Find the magnitude of the force exerted on the strut by the pivot in the arrangement (a).
Forces acting on strut must sum to zero:
(we’re calling the force by the wall on the strut $A$)

$$\Sigma F_y=0=-2w+A_y$$ $$A_y=2w$$ $$\Sigma F_x=0=-T+A_x$$ $$A_x=3/2wcot(\theta )$$ $$|A|=\sqrt{(2w{)}^2+(1.5wcot(\theta ){)}^2}$$

(This one wants it in radians for some reason)

Find the tension T in the cable in the arrangement (b).

$$\Sigma \tau =0=Tsin(15)-0.5wsin(45)-wsin(45)$$ $$T=\frac{0.5wsin(45)+wsin(45)}{sin(15)}$$ $$T=4.12w$$

Find the magnitude of the force exerted on the strut by the pivot in the arrangement (b).

$$\Sigma F_x=0=-4.12wcos(30)+A_x$$ $$A_x=4.12wcos(30)$$ $$\Sigma F_y=0=-4.12wsin(30)-2w+A_y$$ $$A_y=2w+4.12wsin(30)$$ $$|A|=\sqrt{(2w{)}^2+(4.12wcos(30){)}^2}$$

Fuck that:

6 - Easier version of 5

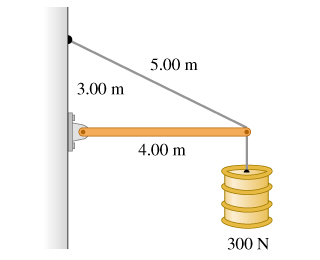
Find the tension in the cable.

$$\Sigma T=0=-75-300+T(3/5)$$ $$T=\frac{375}{3/5}$$ $$T=625$$

Find the horizontal component of the force exerted on the beam at the wall.

$$A_x=T(4/5)$$ $$A_x=625\ast (4/5)=500$$

Find the vertical component of the force exerted on the beam at the wall.

$$A_y=375-300-150=75$$

7

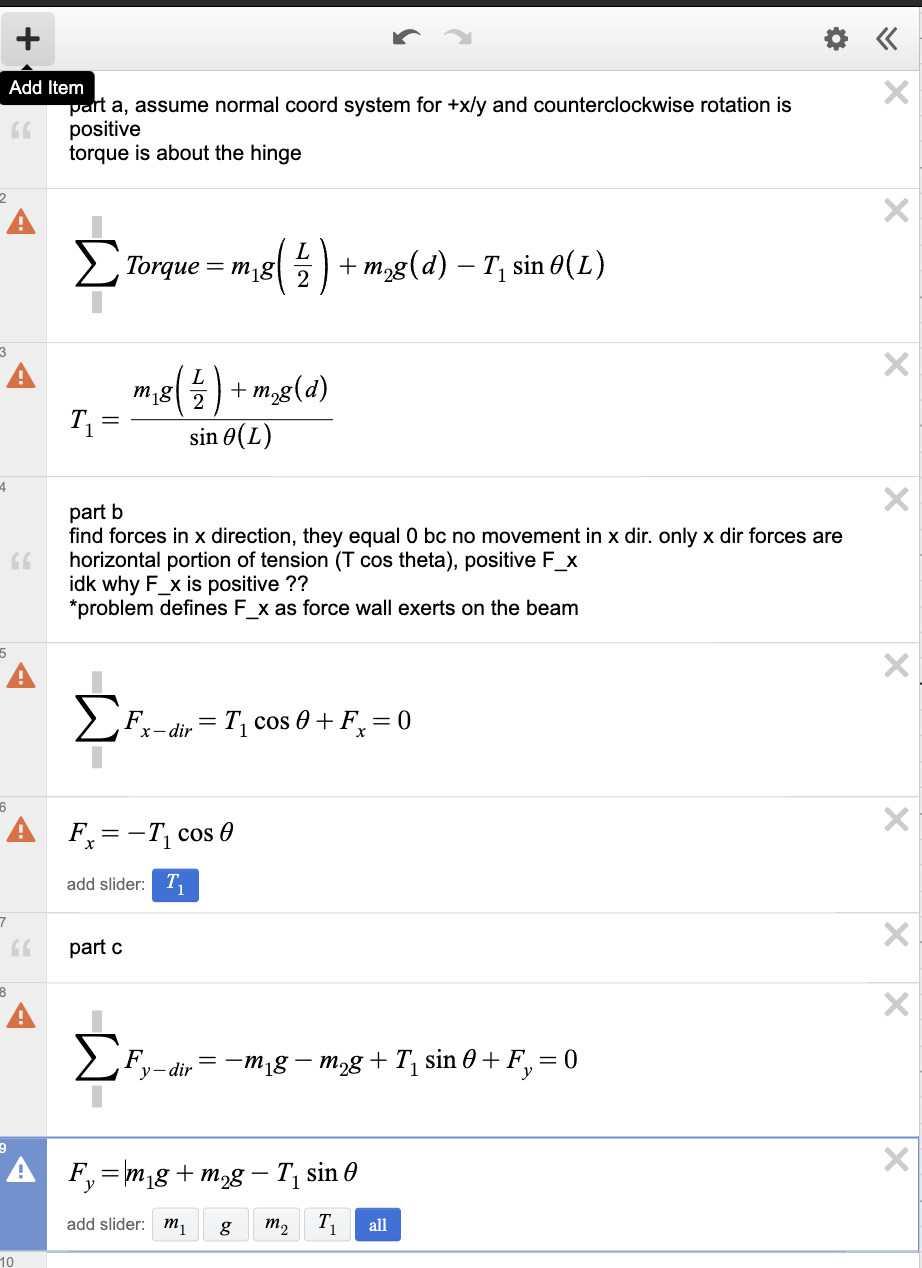
8 - A crane

A 15000-N crane pivots around a friction-free axle at its base and is supported by a cable making a 25 degree angle with the crane (the figure (Figure 1)). The crane is 16 m long and is not uniform, its center of gravity being 7.0 m from the axle as measured along the crane. The cable is attached 3.0 m from the upper end of the crane.

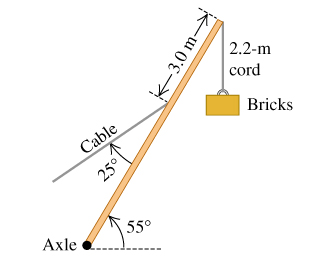When the crane is raised to 55 degrees above the horizontal holding an 11000-N pallet of bricks by a 2.2-m very light cord, find the tension in the cable.

Find the horizontal component of the force that the axle exerts on the crane.

$$\Sigma F_x=0=-cos(55-25)T+A_x$$ $$A_x=\cos (55-25)(2.9\cdot 10^4)=25114.73$$ $$\Sigma F_y=0=A_y-15000-11000-T\sin (55-25)$$ $$A_y=15000+11000+T\sin (55-25)=26000$$

9 - Da armd

 If you have set the tension in the cable to 36.0N on each arm, what is the tension in each deltoid muscle if you simply hold your outstretched arms in place? pivot point is axle, standard axes to hold arm straight (equilibrium) tension in deltoid must = tension in cable
 

$$\Sigma {\tau }_{axle}=T_{cable}(d_{cable})(sin(125))-T_{deltoid}(d_{deltoid})\sin (12)=0$$

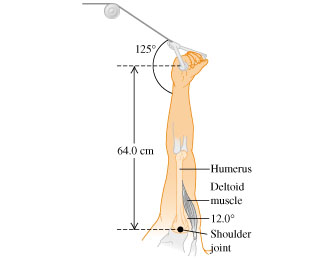
plug in numbers make sure to convert cm to m

$$T_{cable}(d_{cable})(sin(125))=T_{deltoid}(d_{deltoid})sin(12)$$ $$36(0.64)(sin(125))=T_{deltoid}(0.15)sin(12)$$ $$=T_{deltoid}=\frac{36(0.64)(sin(125))}{(0.15)sin(12)}$$ $$T_{deltoid}=605N$$

10 - Some ladder thing

Part A
pivot about top of ladder, standard axes

$$\sum \tau =N2g(L\cos \theta )-f(L\sin \theta )-m2g\left(\frac{L}{2}\cos \theta \right)-m1g((L-d)\cos \theta )=0$$

$N_2=(m_1+m_2)g$
$f=\mu minN2$; $\mu min=f/N2$
^ sub in
im too lazy to do the algebra out but here is the answer

$$\mu min=\frac{m2\cdot \frac{L}{2}\cdot cos(\theta )+m1dcos(\theta )}{(m1+m2)(L\sin \theta )}$$

Part B

Chapter 11 Part B

1 - Crowbar

A nail is hammered into a board so that it would take a force $Fnail$, applied straight upward on the head of the nail, to pull it out. (Take an upward force to be positive.)

A carpenter uses a crowbar to try to pry it out. The length of the handle of the crowbar is $L_h$, and the length of the forked portion of the crowbar (which fits around the nail) is $L_n$. Assume that the forked portion of the crowbar is perfectly horizontal. The handle of the crowbar makes an angle $\theta$ with the horizontal, and the carpenter pulls directly along the horizontal.

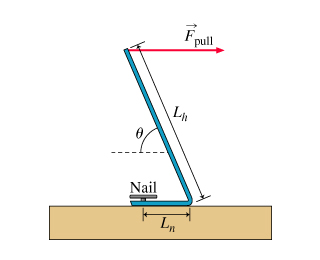
With what force $F_{pull}$ must the carpenter pull on the crowbar to remove the nail? Express the force in terms of $F_{nail}$, $L_h$, $L_n$, and $\theta$.

Torque needed to pull the nail out:

$$\tau =F_{nail}{L}_n$$

Torque by $F_{p}ull$:

$$\tau =F_{pull}sin(\theta )L_h$$

Algebra:

$$F_{nail}{L}_n=F_{pull}sin(\theta )L_h$$ $$F_{pull}=\frac{F_{nail}{L}_n}{sin(\theta )L_h}$$

What is the magnitude of the normal force that the surface exerts on the crowbar, $F_{bar}$? Express your answer for the normal force in terms of $F_{pull}$, $\theta$, $L_n$, and $L_h$. Take the upward direction to be positive.

Torque about the nail is:

$$\tau =F_{pull}(L_{h}sin(\theta ))$$

Torque by normal force at contact point:

$$\tau =F_{bar}{L}_n$$

Torque equilibrium:

$$F_{pull}(L_{h}sin(\theta ))=F_{bar}{L}_n$$ $$\frac{F_{pull}(L_{h}sin(\theta ))}{L_n}=F_{bar}$$

2 - Dresser

Sam is trying to move a dresser of mass $m$ and dimensions of length $L$ and height $H$ by pushing it with a horizontal force $F$ applied at a height $h$ above the floor. The coefficient of kinetic friction between the dresser and the floor is ${\mu }_k$ and $g$ is the magnitude of the acceleration due to gravity. The ground exerts upward normal forces of magnitudes $N_P$ and $N_Q$ at the two ends of the dresser. Note that this problem is two dimensional.

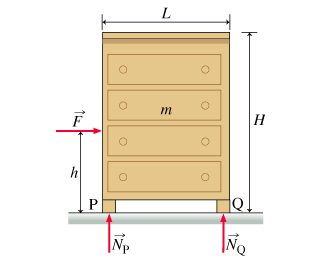
If the dresser is sliding with constant velocity, find $F$, the magnitude of the force that Sam applies. Express the force in terms of $m$, $g$, and ${\mu }_k$.

Since F is horizontal, only $mg$ can contribute to normal and thus friction force.

$$F=mg{\mu }_k$$

Find the magnitude of the normal force $N_P$. Assume that the legs are separated by a distance $L$, as shown in the figure. Express this normal force in terms of $m$, $g$, $L$, $h$, and ${\mu }_k$.

Torque equilibrium about $N_Q$:

$$\Sigma \tau =0=Fh+N_{p}L-mg(0.5L)$$ $$N_{p}L=0.5mgL-Fh$$ $$N_p=\frac{0.5mgL-mg{\mu }_{k}h}{L}$$

Find the magnitude of the normal force $N_Q$. Assume that the legs are separated by a distance $L$, as shown in the figure. Answer in terms of $m$, $g$, ${\mu }_k$, $h$, and $L$.
The sum of the normal forces must equal mg, so

$$N_Q=mg-\frac{0.5mgL-mg{\mu }_{k}h}{L}$$

Find $h_{max}$, the maximum height at which Sam can push the dresser without causing it to topple over. Express your answer for the maximum height in terms $L$ and ${\mu }_k$.

The dresser will topple if the torque due to F is greater than the torque due to gravity

$$F{h}_{max}=0.5mgL$$ $$h_{max}=\frac{0.5mgL}{mg{\mu }_k}$$ $$h_{max}=\frac{0.5L}{{\mu }_k}$$

3 - A rope

A nylon rope used by mountaineers elongates $1.10m$ under the weight of an $65kg$ climber.

If the rope is $45.0m$ in length and $7.0mm$ in diameter, what is Young’s modulus for this material?

$$E=\frac{F/A}{\Delta h/h_0}$$ $$E=\frac{65g/\pi 0.0035^2}{1.1/45}$$

4 - A post

A vertical solid steel post of diameter $d=27cm$ and length $L=2.90m$ is required to support a load of mass $m=8100kg$. You can ignore the weight of the post. Take free fall acceleration to be $g=9.8m$.

What is the stress in the post?
Load over cross sectional area:

$$\frac{mg}{\pi (0.5d{)}^2}$$ $$\frac{8100(9.81)}{3.14(0.5(0.27){)}^2}=1388535.031$$

What is the strain in the post?
Stress over young’s modulous

$$\frac{1388535}{20(10^{10})}=0.000006942675$$

What is the change in the post’s length when the load is applied?
Strain times initial length

$$0.000006942675(2.9)=0.0000201337575$$

5 - Dual rods

Two round rods, one steel and the other copper, are joined end to end. Each rod is $0.750m$ long and $1.50cm$ in diameter. The combination is subjected to a tensile force with magnitude $4000N$.

For the steel rod, what is the strain?
Stress over young’s modulus

$$\frac{4000/\pi 0.0075^2}{20\times 10^{10}}=0.000113$$

For the steel rod, what is the elongation?
Strain times length

$$0.000113\times 0.75=0.00008475$$

6 - Bones underwater

The bulk modulus for bone is $15.0GPa$ .

If a diver-in-training is put into a pressurized suit, by how much would the pressure have to be raised (in atmospheres) above atmospheric pressure to compress her bones by 0.150% of their original volume?

$$E=15000000000\times 0.0015=22500000Pa$$ $$1atm=101325Pa$$ $$22500000/101325=222.057735011atm$$

How many meters does she have to dive?

$$22500000/10000=2250$$

7 - Me when oil is a compressible fluid

A specimen of oil having an initial volume of $650c{m}^3$ is subjected to a pressure increase of $4.0MPa$ , and the volume is found to decrease by $0.50cm3$ .

What is the bulk modulus of the material?
Strain:

$$0.5/650=0.00076923$$

Pressure times strain is bulk modulus:

$$4000000/0.00076923=5200005200$$

8 - Sir lancealot

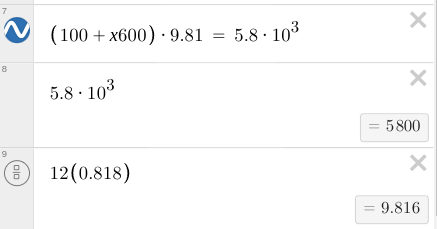(Do the desmos fudge to find x, which for me wa 0.818), also the problem is the same for everyone
(The real way to do this is with torque equilibrium)

9 - Rock

A museum of modern art is displaying an irregular 426-N sculpture by hanging it from two thin vertical wires, A and B, that are 1.25 mm apart (the figure (Figure 1)). The center of gravity of this piece of art is located 48.0 cm from its extreme right tip.

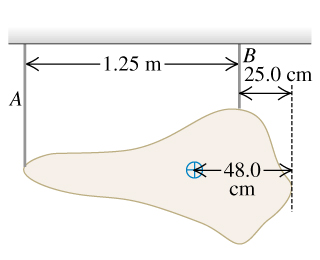
Find the tension in the wire A.
Find the tension in the wire B.

Linear force equilibrium:

$$\Sigma F=0=T_A+T_B-mg$$

Torque Equlibrium: (clockwise positive, about B)

$$\Sigma \tau =0=T_A{d}_{AB}-mg{d}_{r_{c}B}$$

Sub in:

$$0=T_A(1.25)-(426)(0.48-0.25)$$ $$T_A=\frac{(426)(0.48-0.25)}{(1.25)}=78.384N$$

Sub $T_A$ into the force equilibrium and solve for $T_B$

$$T_B=mg-T_A$$ $$T_B=426-78.384=347.616N$$

10 - Meter stick

One end of a uniform meter stick is placed against a vertical wall. The other end is held by a lightweight cord that makes an angle θ with the stick. The coefficient of static friction between the end of the meter stick and the wall is 0.37.

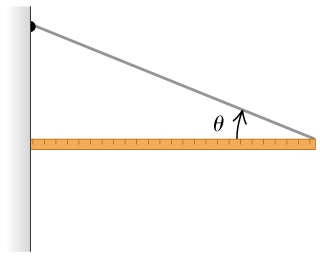What is the maximum value the angle θ can have if the stick is to remain in equilibrium?

Linear force equilibrium:

$$\Sigma F_x=0=N-Tcos(\theta )$$ $$\Sigma F_y=0={\mu }_{k}N+Tsin(\theta )-W$$

Torque equilibrium: (clockwise positive) about string end of stick

$$\Sigma \tau =0={\mu }_{k}N-0.5W$$ $$W=2{\mu }_{k}N$$

Combine eq for $\Sigma F_y$ and $W$:

$$\Sigma F_y=0={\mu }_{k}N+Tsin(\theta )-2{\mu }_{k}N$$

Solve $\Sigma F_x$ for $N$ and sub in:

$$\Sigma F_y=0={\mu }_{k}Tcos(\theta )+Tsin(\theta )-2{\mu }_{k}Tcos(\theta )$$ $$\Sigma F_y=0={\mu }_{k}cos(\theta )+sin(\theta )-2{\mu }_{k}cos(\theta )$$ $$\Sigma F_y=0=sin(\theta )-{\mu }_{k}cos(\theta )$$ $${\mu }_k=\frac{sin(\theta )}{cos(\theta )}$$ $$0.37=\frac{sin(\theta )}{cos(\theta )}$$

Let the angle between the cord and the stick is $\theta =18$. A block of the same weight as the meter stick is suspended from the stick, as shown at, at a distance x from the wall. What is the minimum value of x for which the stick will remain in equilibrium?

Linear force equilibrium:

$$\Sigma F_x=0=N-Tcos(\theta )$$ $$\Sigma F_y=0={\mu }_{k}N+Tsin(\theta )-2W$$ $$W=\frac{{\mu }_{k}N+Tsin(\theta )}{2}$$

Torque equilibrium: (clockwise positive) about string end of stick (the stick is.. you know.. one meter long)

$$\Sigma \tau =0={\mu }_{k}NL-0.5LW-((1-x)/L)W$$ $$-{\mu }_{k}N=(-0.5+(1-x))W$$ $$\frac{{\mu }_{k}N}{W}+0.5=x$$ $$\frac{2{\mu }_{k}cos(\theta )}{{\mu }_{k}cos(\theta )+sin(\theta }+0.5=x$$

RIP that’s wrong…
It’s 43.5 cm

and 0.74 (but this one is diff for everyone)

12 - Goofy wah useless stupid stick thing

12 A

6 - Dam

Part B

12 - Dual fluid block equilibrium

12B

8 - scuffed wood block

A cubical block of wood $0.100m$ on a side and with a density of $550kg/m^3$ floats in a jar of water. Oil with a density of $750kg/m^3$ is poured on the water until the top of the oil layer is $0.035m$ below the top of the block.

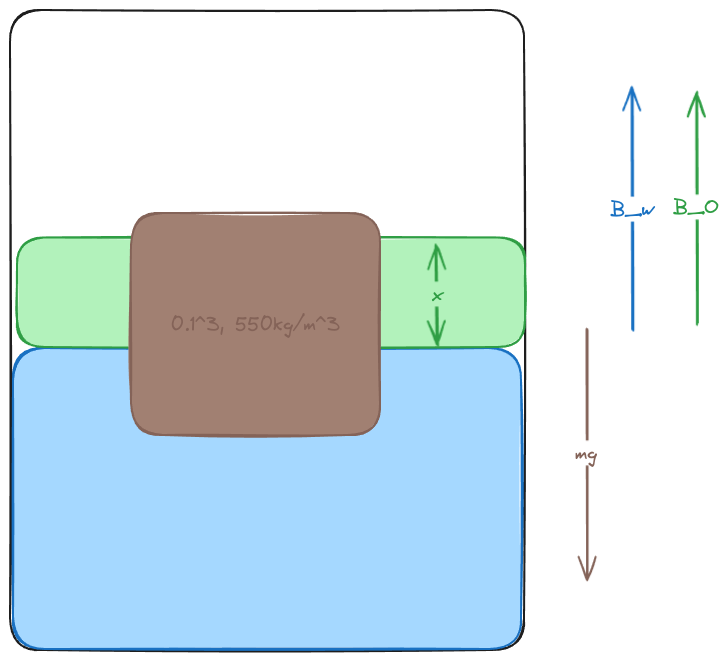How deep is the oil layer?

$$mg=B_w+B_O$$ $$(550\ast 0.1^3)g=750(0.1^2)xg+1000(0.1^2)((0.1-0.035)-x)g$$ $$x=4\times 10^{-2}$$

What is the gauge pressure at the block’s lower face?

$$p=p_0+\rho gh$$ $$p={\rho }_{W}g(0.1-0.035-4\times 10^{-2})+{\rho }_{O}g4\times 10^{-2}=539.55Pa$$

9 - high precision buoutancy calculatoins of hilariously tiny boat

10 - tank can’t decide where to make the fricking holes

Ch 14A

8 - Sewing machine

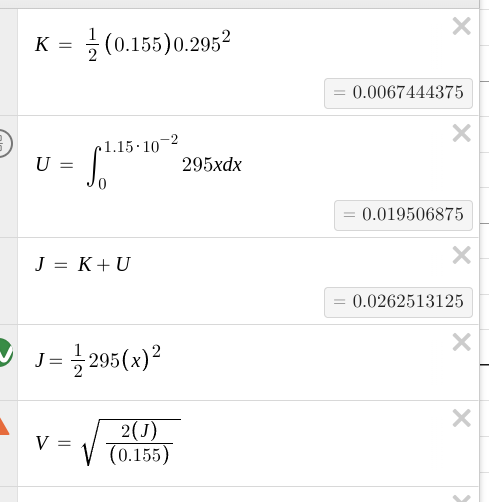
The point of the needle of a sewing machine moves in SHM along the xx-axis with a frequency of 2.5 Hz. At t=0 its position and velocity components are +1.1cm and −15cm/s.
Find the acceleration component of the needle at $t=0$.

$$\omega =2.5\ast 2\pi =15.707$$ $$a(t)=-{\omega }^{2}A\cos (\omega t)$$

$A\cos (\omega t)$ is the displacement, but since we know that, we can just sub it in.

$$a(t)=-{\omega }^2(1.1)$$ $$a(t)=-15.707^2(0.011)=-2.71$$

Write an equation giving the position component of the point as a function of time.

$$x(t)=A\cos (\omega t)$$

10 - idek

11

12

Ch 16

Item 6

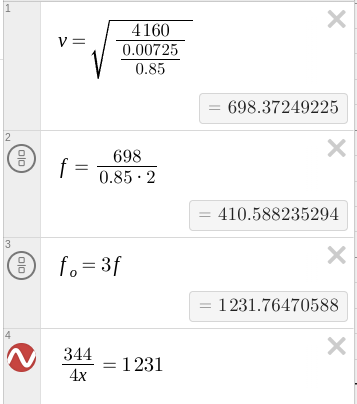
You have a stopped pipe of adjustable length close to a taut 85.0-cmcm, 7.25-gg wire under a tension of 4160 NN . You want to adjust the length of the pipe so that, when it produces sound at its fundamental frequency, this sound causes the wire to vibrate in its second overtone with very large amplitude.
How long should the pipe be?