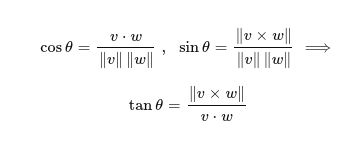Vectors

Always i, j , k

|a| = amplitude of vector a

i_x j_x
i_y j_y

Representing Vectors

R^n

Set of lists of n numbers
R^1 is a vector space which is a list of all single numbers

Geometrically

Arrows but without coordinates

Arrows with coordinates

Unit Vectors

(x, y, z)
i^ = (1, 0, 0)
j^ = (0, 1, 0)
k^ = (0, 0, 1)

Cross products

i^ x j^ = +1

$$|a\times b|=|a||b|sin(\theta )$$

Determinate

Measures how area or volume changes with a linear transformation

[a b]
[c d] = ad-bc

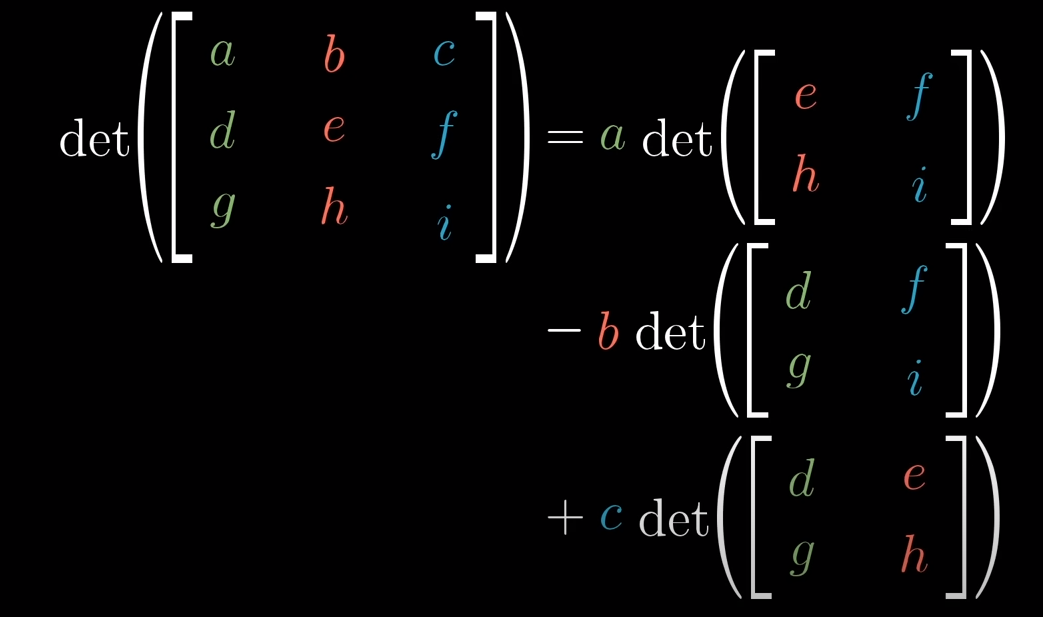
Dot products

• Multiply corresponding elements of vector
• Sum resulting coefficients/amplitudes
• Amplitudes that don’t exist are 0, and multiplication rule holds true

$$a=3j+2k,b=2j$$ $$a\cdot b=(3\ast 2)$$

Other rules

Vectors are orthogonal when their dot product is zero

$$a\cdot b=|a||b|cos(\theta )$$

$$a\cdot a=|a{|}^2$$

Matrix Multiplication

• undefined when number of columns of first matrix don’t match number of rows of second matrix

print("[a b] [e f]\n[c d] [g h]")    
a = int(input("a: "))    
b = int(input("b: "))    
c = int(input("c: "))    
d = int(input("d: "))    
e = int(input("e: "))    
f = int(input("f: "))    
g = int(input("g: "))    
h = int(input("h: "))    
alpha = (a*e) + (b*g)    
beta = (a*f) + (b*h)    
carrot = (c*e) + (d*g)    
delta = (c*f) + (d*h)    
print("[", alpha, " ", beta, "]\n[", carrot, " ", delta, "]")  

Composition of Transformations

Matrices aren’t associative so you have to do it the right way around

$$B(A(x))where{M}_1=Aand{M}_{2}isB$$

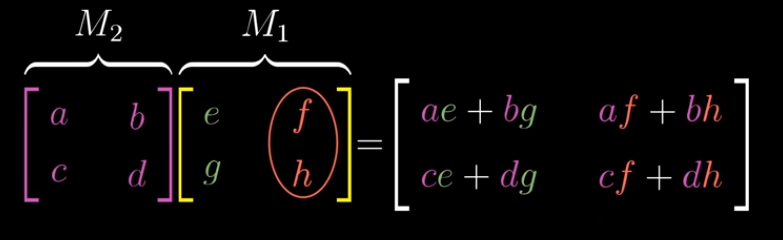
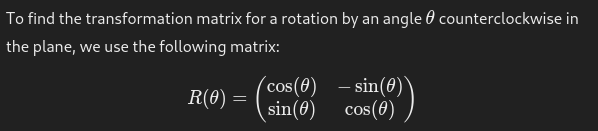
Transposition (X^T)

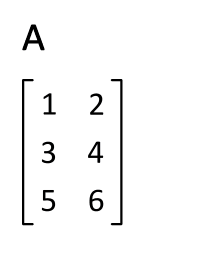
Generalized Transformations

Counterclockwise R^3 about the x axis

.

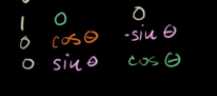
General or Non-Conforming Rules