Work, Energy, Torque

Momentum - Center of Mass Theorem

The linear momentum of a system of particles is equal to the product of the total mass M of the system and the velocity of the center of mass.

Collisions

Inelastic: Momentum is conserved
Elastic: Kinetic energy and momentum is conserved

On any path, a force constant in magnitude and direction will do the same amount of work

Equations

Linear Motion

Energy

Work ($J$), as a function of distance ($m$) and force ($N$), where $\theta$ is the angle between distance and force:

$$W=Fdcos(\theta )$$ $$W={\int }_A^B\vec{F}\cdot d\vec{l}$$

Linear kinetic energy, $K$ ($J$) as a function of mass ($kg$) and velocity ($m/s$):

$$K=0.5m{v}^2$$

Above, rewritten for velocity in terms of energy and mass:

$$v=\sqrt{\frac{2K}{m}}$$

Gravitational Potential energy, U, (J) in terms of mass, gravitational constant, and height

$$\Delta U=mgh$$

Only non conservative forces can change the total energy of an object or system:

$$W_{nc}=U_i+K_i-U_f-K_f$$

Force in each direction is equal to the change in potential energy over the change in position in that direction:

$$F_x=\frac{\delta U}{\delta x}$$ $$F_y=\frac{\delta U}{\delta y}$$ $$F_z=\frac{\delta U}{\delta z}$$

The disassociation energy of a system is it’s final potential energy less it’s origin potential energy:

$$U_{dis}=U_{\infty }-U_r$$

Momentum

$P$ = momentum in $kgm/s$
$m$ = mass in kg
$v$ = velocity in m/s

$$P=mv$$ $$\Delta P=m\Delta v$$ $$\Delta P=J$$

Impulse (newton seconds) =
$J$ = impulse in $kgm/s$
$F$ = force in N

$$J=Ft$$ $$J=m\Delta v$$

Angular Motion

Moments of Inertia

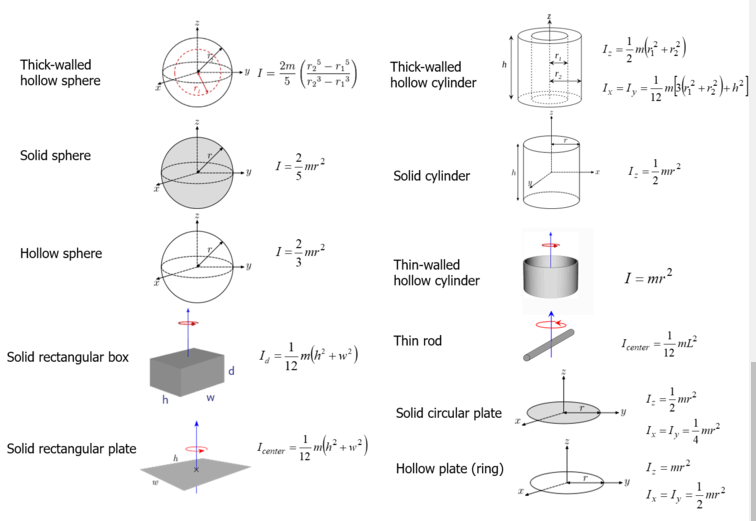Parallel Axis Theorum: (when things are rotating not about their center)

The moment of inertia of a thing not rotating about it’s center is equal to it’s moment of inertia about it’s center plus it’s moment of inertia as if it were a particle

$$I=I_{CM}+M{L}^2$$

Finding Torque

Radius and tangential component of force:

$$\tau =r{F}_{tan}$$

Lever arm (perpendicular distance between line of force and rotation center) and Force:

$$\tau =lF$$

Vector cross product of torque and point of action:

$$\vec{\tau }=\vec{r}\vec{F}$$

Energy

Rotational kinetic energy, $K$ (J) in terms of angular velocity, $\omega$, (rad/s ) and moment of inertia, $I$ ($kg{m}^2$ but not $J$):

$$K=\frac{1}{2}I{\omega }^2$$ $$I=\frac{2K}{{\omega }^2}$$

Torque as a function of angular acceleration ($rad/s^2$) and moment of inertia:

$$\Sigma \tau =I\alpha$$

Momentum

Angular momentum (L) as a function of moment of inertia and angular velocity $\omega$

$$L=I\omega$$

Torque is the change in angular momentum:

$$\tau =\frac{\Delta L}{\Delta t}$$

Precession

Angular velocity of precession ${\omega }_P$ is magnitude of torque on gyroscope over angular momentum of gyroscope

$${\omega }_P=\frac{|\tau |}{|L|}$$