Complex Numbers in Linear Algebra

$C$: Set of all complex numbers if $z\in C$ then $z=a+bi$, $a,b\in R$

Modulus: Trig length: $|z|=\sqrt{a^2+b^2}$
Argument: The angle the modulus vector makes with the positive real axis. $Arg(z)=\arctan \frac{im}{re}$
Polar Form: $z=|z|\cos \theta +|z|i\sin \theta$
Conjugate: $z=a+bi\to \overline{z}=a-bi$

Euler’s Formula: $e^{i0}=cos(\theta )+isin(\theta )\to e^z=e^a\cos b+i{e}^a\sin b$

Finding Eigenvalues: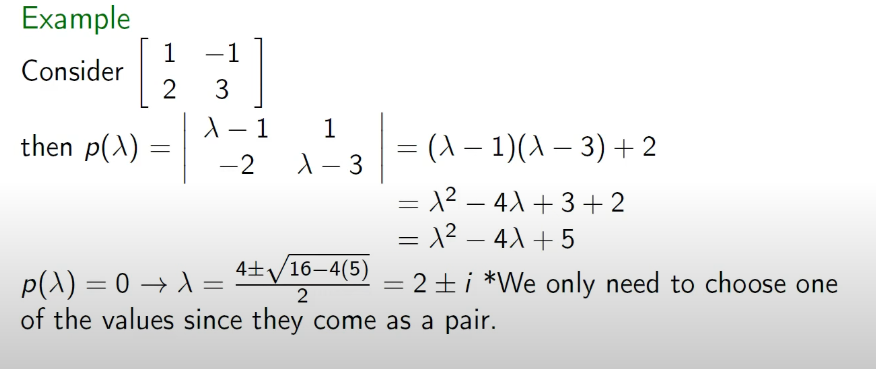

Finding Eigenvectors: Make matrix where 11 and 22 are their value minus the complex eigenvalue, then rref. take negative of result and if it’s in the second column, it goes first followed by a 1. If it’s in the first column, it goes second proceeded by a 1. To get the conjugate, invert the sign of the complex part.

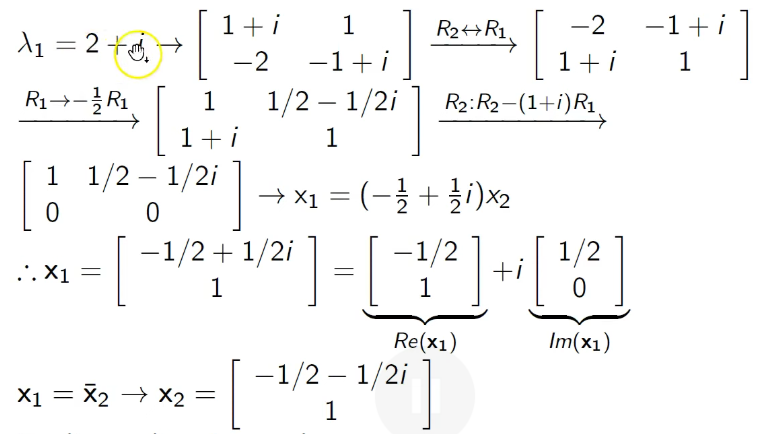
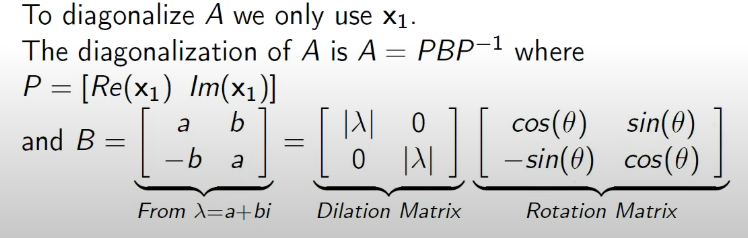
Getting Dilation and Rotation:
Rotation: $\theta =\arccos \frac{a}{|\lambda |}$
Dilation: $|\lambda |$

Example of finding Eigenvalue, Eigenvector, Rotation, and Dilation:

Consider $\left[\begin{array}{cc}3& -2\\ 2& 3\end{array}\right]$
From Matricies, we know

$\lambda =m\pm \sqrt{m^2-p}$ where m is the mean of the trace: $\frac{a+c}{2}$ and p is the determinate

$$\lambda =3\pm \sqrt{9-13}$$ $$\lambda =3\pm 2i$$

Using only $\lambda =3+2i$, we can find eigenvector and it’s conjugate:
Subtract $\lambda$ from 11 and 22:

$$\left[\begin{array}{cc}3-3-2i& -2\\ 2& 3-3-2i\end{array}\right]\to \left[\begin{array}{cc}-2i& -2\\ 2& -2i\end{array}\right]$$

Calculator

$$\text{rref}\left[\begin{array}{cc}-2i& -2\\ 2& -2i\end{array}\right]=\left[\begin{array}{cc}1& -i\\ 0& 0\end{array}\right]$$

Since non-one value is on the right, it goes on the top of the vector (don’t ask idk), also sign get’s flipped

$$x_1=\left[\begin{array}{c}i\\ 1\end{array}\right]$$

Dilation is the modulus of $\lambda$, $|\lambda |=\sqrt{13}$
We know $P=\left[\begin{array}{cc}a& b\\ -b& a\end{array}\right]$ (From standard form of complex number)
We also know $P=\left[\begin{array}{cc}|\lambda |& 0\\ 0& |\lambda |\end{array}\right]\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]$
So.. the first operation of multiplying those is $\cos \theta |\lambda |=a$, or: $\theta =\arccos \frac{a}{|\lambda |}$

$$\theta =\arccos \frac{3}{\sqrt{13}}=0.588$$