3.1 Linear Transformations

1. Find the image of the vector $\mathbf{u}$ under the linear transformation $T(\mathbf{x})=A\mathbf{x}$ where:

a. $A=\left[\begin{array}{ll}3& 4\\ 0& 2\end{array}\right],\mathbf{u}=\left[\begin{array}{c}4\\ -1\end{array}\right]$

$$\left[\begin{array}{c}8\\ -2\end{array}\right]$$

b. $A=\left[\begin{array}{cc}1& 3\\ -1& 0\\ 3& 3\end{array}\right],\mathbf{u}=\left[\begin{array}{c}3\\ -2\end{array}\right]$

$$\left[\begin{array}{c}-3\\ -3\\ 3\end{array}\right]$$

2. Determine if $\mathbf{v}$ is in the range of…

$T(\mathbf{x})=A\mathbf{x}$ where $A=\left[\begin{array}{ccc}3& 0& -1\\ 1& 2& 3\end{array}\right],\mathbf{v}=\left[\begin{array}{l}4\\ 2\end{array}\right]$

$$\left[\begin{array}{ccc}3& 0& -1\\ 1& 2& 3\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}4\\ 2\end{array}\right]$$ $$\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}4/3+s/3\\ 1/2-2s/3\\ s\end{array}\right]$$

3. Show that the function..

$T:{\mathbf{R}}^2\to {\mathbf{R}}^2$ is not a linear transformation: $T\left(\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]\right)=\left[\begin{array}{c}2x_2{}^2\\ x_1+1\end{array}\right]$

1. The zero vector does not result in a zero output
2. There’s a square, so it can’t be linear unless there’s something to cancel it out, which there isn’t.

4. Determine if the linear transformation..

$T:{\mathbf{R}}^{\mathrm{m}}\to {\mathbf{R}}^{\mathrm{n}}$ given by $T(\mathbf{x})=A\mathbf{x}$ is one-to-one. Similarly, determine if it is onto.
a. $A=\left[\begin{array}{ll}2& 1\\ 1& 1\end{array}\right]$
One-to-one and onto
b. $A=\left[\begin{array}{ccc}3& 0& -1\\ 1& 2& 3\end{array}\right]$
onto
c. $A=\left[\begin{array}{cc}1& 3\\ -1& 0\\ 3& 3\end{array}\right]$
one-to-one

5. Find the matrix $A$ such that the linear transformation…

$T:{\mathbf{R}}^3\to {\mathbf{R}}^2$ is given by $T(\mathbf{x})=A\mathbf{x}$ :

$$T\left(\left[\begin{array}{l}{x}_1\\ x_2\\ x_3\end{array}\right]\right)=\left[\begin{array}{c}2x_3-x_1+2x_2\\ x_1+x_2\\ 3x_1-5x_2-3x_3\end{array}\right]$$ $$A=\left[\begin{array}{ccc}-1& 2& 2\\ 1& 2& 0\\ 3& -5& -3\end{array}\right]$$

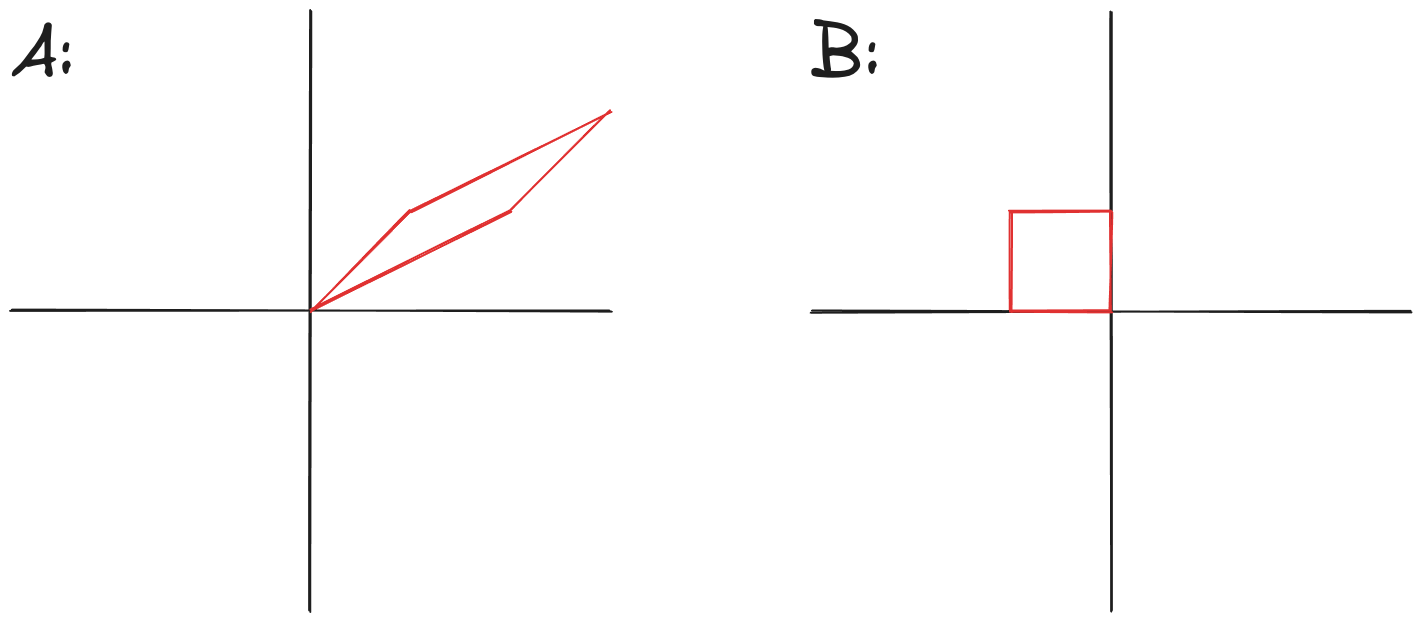
6. Graph the image of the unit square…

in the first quadrant under the linear transformation $T:{\mathbf{R}}^2\to {\mathbf{R}}^2$ is given by $T(\mathbf{x})=A\mathbf{x}$ :
a. $A=\left[\begin{array}{ll}2& 1\\ 1& 1\end{array}\right]$
b. $A=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$

7. Suppose that $T$ is a linear transformation..

and that ${\mathbf{u}}_1$ and ${\mathbf{u}}_2$ are linearly dependent. Prove that $T\left({\mathbf{u}}_1\right)$ and $T\left({\mathbf{u}}_2\right)$ are also linearly dependent.

If $u_1$ and $u_2$ are scalar multiples of one another, then no matter what you multiply them by, so long as it’s the same for both of them, they will maintain their relationship.

8. Prove that $T\left(x_1,x_2,x_3\right)=\left[x_1,x_2\right]$ is a linear transformation.

This can satisfy both additivity and homogeniety, so it is a linear transformation.