Matricies

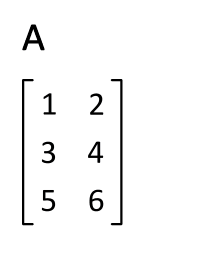
See also Vectors and Vectors

Augmented Matrix: A matrix where each row is an equation, and each column is the coefficients for a particular variable in each equation. For example:

$$\begin{array}{rl}6x_1+x_2-3x_4& =11\\ 3x_2-4x_3+5x_4& =6\\ 2x_3-4x_4& =-3\end{array}\to \left[\begin{array}{cccccc}6& 1& 0& -3& |& 11\\ 0& 3& -4& 5& |& 6\\ 0& 0& 2& -4& |& -3\end{array}\right]$$

Gaussian Elimination: Using elementary row operations to put a matrix in echelon form

Gauss-Jordan Elimination: Using elementary row operations to put a matrix in reduced echelon form

Reduced Echelon Matrix: A matrix is in reduced row echelon form (also called row canonical form) if it satisfies the following conditions:

1. It is in row echelon form.
2. The leading entry in each nonzero row is 1 (called a leading one).
3. Each column containing a leading 1 has zeros in all its other entries. Steps:
4. Make $a_{11}$ 1
5. Make everything below $a_{11}$ zero
6. Repeat with $a_{22}$

Free Variable: A variable that can’t be eliminated or constrained. Happens when you have more variables than equations.

LU Decomposition: use elementary row operations to create a lower and upper triangular matrix which together are equivalent to a coefficient matrix

Rank: A way of describing the dimensionality of the output of a transformation. If a transformation outputs a line, the rank is 1, an area: rank 2, and a volume: rank 3. Number of linearly independent columns, or rows, whichever the matrix has fewer of.

Column Space: The range of all possible outputs of a transformation. Equal to the span of the columns of the matrix, if they are treated as vectors. Column Space Basis: The columns from the original matrix which have pivots in the REF of that matrix

Row Space Basis: REF the matrix and pick out the non-zero rows (From the original Matrix (At least in mcmillan))

Nullitity: Columns - Rank

Null Space / Kernel: The set of all inputs to the linear transformation who’s output is the origin.

Null Space Basis: RREF, then write the non zero rows, but with any free variables negative

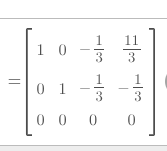
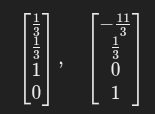
Cofactor: The determinate of the matrix with the row and column of the mentioned cell removed.

Eigenvector: Becomes a scalar multiple of itself when a given operator is applied to it. Find from eigenvalue using equation $(A-\lambda I)v=0$ See also, example of complex eigenvector

Eigenvalue: The amount a particular eigenvector get’s stretched for 2x2 matricies, $m\pm \sqrt{m^2-p}$ where m is the mean of the trace: $\frac{a+c}{2}$ and p is the determinate See also, example of complex eigenvalue

Diagonalization: Change basis so transformation is a diagonal matrix and becomes light work

• $PD{P}^{-1}$
• P is change of basis matrix
• D is new diagonal matrix
• For a matrix to be diagonolizable, there need to be at least as many eigenvectors as there are rows

Change of Basis Matrix: To go from any basis to the standard basis, literally put the basis as a matrix. To go from standard to a different basis, write the new basis as a matrix, and calculate it’s inverse. To go between two basis, get the product of the inverse of the second basis X the first basis. $A\to B:B^{-1}A$

If they aren’t square you do this shit: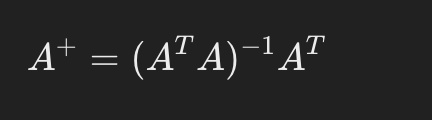

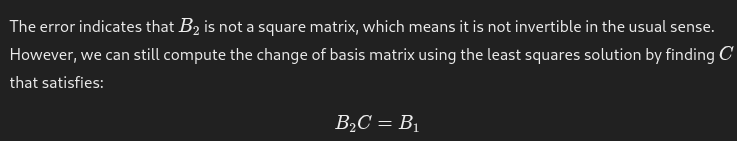
Inverses

When determinate is not equal to zero:

$$A_{-1}A=I$$

If the determinate is zero, there is no inverse.

Elementary Row Operations

Equivalent to operations on systems Interchange Equations: Swap two rows

Multiply an Equation by a Constant: Multiply one row by a constant.. Ex:

$$\left[\begin{array}{cccccc}6& 1& 0& -3& |& 11\\ 0& 3& -4& 5& |& 6\\ 0& 0& 2& -4& |& -3\end{array}\right]\to \left[\begin{array}{cccccc}0& 3& -4& 5& |& 6\\ 6& 1& 0& -3& |& 11\\ 0& 0& 2& -4& |& -3\end{array}\right]$$

Add a multiple of one equation to another: Ex: Row 2 + 2* Row 3 $\to$ Row 2

$$\left[\begin{array}{cccccc}6& 1& 0& -3& |& 11\\ 0& 3& -4& 5& |& 6\\ 0& 0& 2& -4& |& -3\end{array}\right]\to \left[\begin{array}{cccccc}6& 1& 0& -3& |& 11\\ 0& 3& 0& -3& |& 0\\ 0& 0& 2& -4& |& -3\end{array}\right]$$

Application/Problem Types

Wire Temperature

1. Make an equation for each node, temp = average of all connected nodes
2. solve for constant
3. Put into matrix
4. RREF

Balance the Chemical Equation

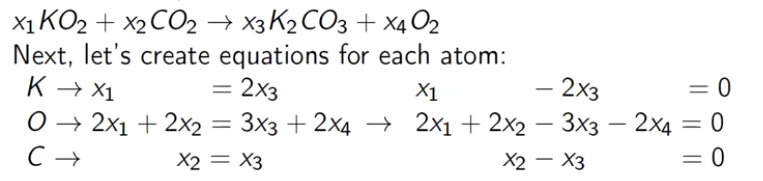
Traffic Management:

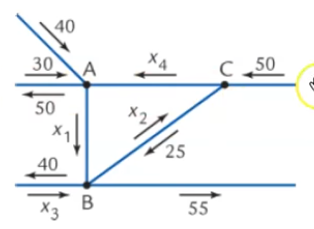
1. Write an equation for each intersection (A,B,C) where one side is the sum of all the input and the other is the side of all the output A: $40+30+x_4=50+x_1$
2. Solve equations for the constant
3. RREF

Find the missing values in the partial fraction decomposition

5. Generate a single, distributed equation 6. Separate each “set of coefficients” (here it’s constants and coefficients of x, but it could be powers of x or different variables (I think)) 7. RREF

Transformations

one-to-one: if A has linearly independent columns (no free vars) onto: if A spans all of $R_n$

Counterclockwise R^3 about the x axis

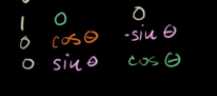
Composition of Transformations

Matrices aren’t associative so you have to do it the right way around

$$B(A(x))where{M}_1=Aand{M}_{2}isB$$

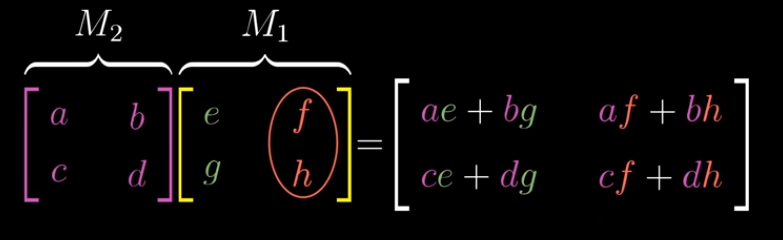
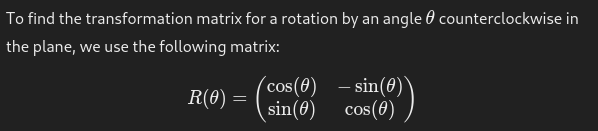
Matrix Multiplication

undefined when number of columns of first matrix don’t match number of rows of second matrix

print("[a b] [e f]\n[c d] [g h]")  
a = int(input("a: "))  
b = int(input("b: "))  
c = int(input("c: "))  
d = int(input("d: "))  
e = int(input("e: "))  
f = int(input("f: "))  
g = int(input("g: "))  
h = int(input("h: "))  
alpha = (a*e) + (b*g)  
beta = (a*f) + (b*h)  
carrot = (c*e) + (d*g)  
delta = (c*f) + (d*h)  
print("[", alpha, " ", beta, "]\n[", carrot, " ", delta, "]")

Transposition (X^T)