1.1 Lines and Linear Equations

1. Three investors, X, Y, Z…

purchased all of the stock (100 shares) from a certain company. For voting purposes, each investor’s vote is multiplied by the number of shares owned. Therefore, if any investor has 51 or more shares, they can control the company. If Investor X buys $\frac{1}{3}$ of Investor’s Y ’s shares, he will have 51. If Investor Z buys $\frac{3}{5}$ of Investor’s X’s shares, she will have 51. How many shares does each investor have?

Given:

$$x+\frac{y}{3}=51$$ $$z+\frac{3}{5}x=51$$ $$x+y+z=100$$

Work:

$$100-y-\frac{2}{5}x=51$$ $$y=49-\frac{2}{5}x$$ $$x+\frac{49-\frac{2}{5}x}{3}=51$$ $$245+13x=765$$ $$x=520/13=40$$ $$z=51-\frac{3}{5}(40)=27$$ $$y=100-40-27=33$$

Answer:
X owns 40 shares initially, y owns 33 shares, and z owns 27 shares.

2. Consider a particle that moves with acceleration…

$$a(t)=\cos (t)$$

and that its position at $\pi$ seconds is $x(\pi )=15$, and its position at $2\pi$ seconds is $x(2\pi )=9$. Find the equation of its position $x(t)$.

Work:
Integral of acceleration is velocity…

$$v(t)=\int \cos (t)=\sin (t)+C$$

Integral of velocity is position…

$$x(t)=\int \sin (t)+C=-\cos (t)+Ct+D$$

Plugin points and solve as system:
Point A:

$$-cos(\pi )+C\pi +D=15$$ $$1+C\pi +D=15$$ $$-1-C\pi +15=D$$

Point B:

$$-cos(2\pi )+2C\pi =9$$ $$-1+2C\pi +D=9$$ $$1-2C\pi +9=D$$

Combine:

$$-1-C\pi +15=1-2C\pi +9$$ $$C=\frac{-4}{\pi }\simeq 1.2732$$

Substitute to solve for D:

$$1+\frac{-4}{\pi }\pi +D=15$$ $$D=18$$

Answer:

$$x(t)=\frac{-4}{\pi }t-\cos (t)+18$$

Trust but verify:

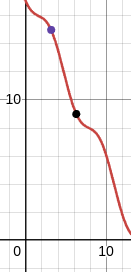
3. Find the point at which the lines…

$8x-4y=18$ and $12x+2y=13$ intersect.
Given:

$$8x-4y=18$$ $$12x+2y=13$$

Work:

$$x=\frac{18}{8}+\frac{y}{2}$$ $$27+6y+2y=13$$ $$y=-\frac{14}{8}$$ $$12x+-\frac{14}{4}=13$$ $$x=\frac{11}{8}$$

Answer:
The intersection of the two lines it located at $(\frac{11}{8},-\frac{14}{8})$

4. Demonstrate that the following sets…

are indeed solutions to the given linear systems.
a. $14x_1+5x_2=13$ $\cap$ $6x_1+2x_2=8$ $\to$ (7, −17)

$$14(7)+5(-17)=13$$ $$6(7)+2(-17)=8$$

b. $3x_1+5x_2+7x_3=14$ $\cup$ $2x_1+4x_3=4$ $\to$ $(-14+10s_1,1,8-5s_1)$

$$2(-14+10s_1)+4(8-5s_1)=4$$ $$20s_1-20s_1=0$$ $$s_1=s_1$$ $$3(-14+10s_1)+5+7(8-5s_1)=4\to s_1=1$$

Answer:
The given to set a is valid, the solution to set b is valid, and $s_1=1$

5. Use back substitution to solve…

the following linear system in triangular form.

$$\begin{array}{rl}2x_1-2x_2+3x_3& =3\\ 3x_2+2x_3& =21\\ 5x_3& =15\end{array}$$ $$x_3=3$$ $$3x_2+2(3)=21\to x_2=5$$ $$2_{x}1+2(5)+3(3)=3\to x_1=-8$$

Answer:
$x_1=-8$, $x_2=5$, $x_3=3$

6. Use back substitution to solve…

the following linear system in echelon form.

$$\begin{array}{rl}6x_1+x_2-3x_4& =11\\ 3x_2-4x_3+5x_4& =6\\ 2x_3-4x_4& =-3\end{array}$$ $$2x_3-4x_4=-3\to x_3=2x_4-\frac{3}{2}$$ $$x_4=\frac{x_3}{2}+\frac{3}{4}$$ $$3x_2-4(2x_4-\frac{3}{2})+5x_4=6\to x_2=x_4$$ $$6x_1+x_2-3x_4=11$$ $$6x_1+x_4-3x_4=11$$

Answer:
The system cannot be fully solved. Expressed in terms of $x_4$, it is solved as:

$$\begin{array}{rl}{x}_1& =\frac{11+2x_4}{6},\\ x_2& =x_4,\\ x_3& =2x_4-\frac{3}{2},\\ x_4& =x_4\text{(free parameter)}.\end{array}$$

7. Use back substitution to solve…

the following linear system in echelon form.

$$\begin{array}{rl}{x}_1+3x_2+3x_4-5x_5& =5,\\ x_3-6x_4+10x_5& =-7,\\ 3x_4-4x_5& =6.\end{array}$$ $$x_4=\frac{4}{3}{x}_5+2$$ $$x_3-6(\frac{4}{3}{x}_5+2)+10x_5=-7$$ $$x_3=5-2x_5$$ $$x_1+3x_2+3(\frac{4}{3}{x}_5+2)-5x_5$$ $$x_1=-1-3x_2+x_5$$

Answer:
The system cannot be fully solved. Expressed in terms of $x_5$ and $x_2$, it is solved as:

$$\begin{array}{rl}{x}_1& =-1-3x_2+x_5,\\ x_2& =x_2\text{(free parameter)},\\ x_3& =5-2x_5,\\ x_4& =\frac{4}{3}{x}_5+2,\\ x_5& =x_5\text{(free parameter)}.\end{array}$$

8. For which values of k…

is the following linear system consistent?

$$\begin{array}{rl}5x_1+x_2& =7,\\ 2x_1+k{x}_2& =2.\end{array}$$ $$5x_1-7=x_2$$ $$2x_1-5k{x}_1+7k=2$$ $$(2-5k)x_1=2-7k$$

If $2-5k\ne 0$, we can solve for $x_1$ and the system will be consistent.
If $2-5k=0$, the system will have infinitely many solutions (if $2-7k=0$) or be inconsistent (if $2-7k\ne 0$).

Answer:
k can be anything except $\frac{2}{5}$