Vectors

Unit Vectors

(x, y, z) i^ = (1, 0, 0) j^ = (0, 1, 0) k^ = (0, 0, 1)

Linear Combinations

The sum of products of a series of vectors and scalars

$$\Sigma \overrightarrow{u_m}{c}_m$$

Span

The span of a set of vectors is the range of vectors you can make by scaling them individually and adding them together, in a linear combination.

• The span of most vectors is the entire space they reside
• The span of parallel vectors is a line
• The span of zero vectors is the origin
• The span of 2 vectors in 3d space is a plane

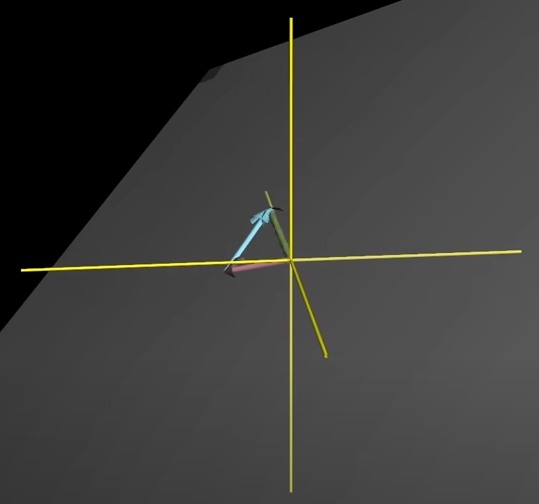
If an additional vector exists in the span of other vectors being considered, the span of the collection does not change. In this case, the new vector is “linearly dependent”.

Cross products

i^ x j^ = +1

$$|a\times b|=|a||b|sin(\theta )$$

Determinate

Measures how area or volume changes with a linear transformation

[a b] [c d] = ad-bc

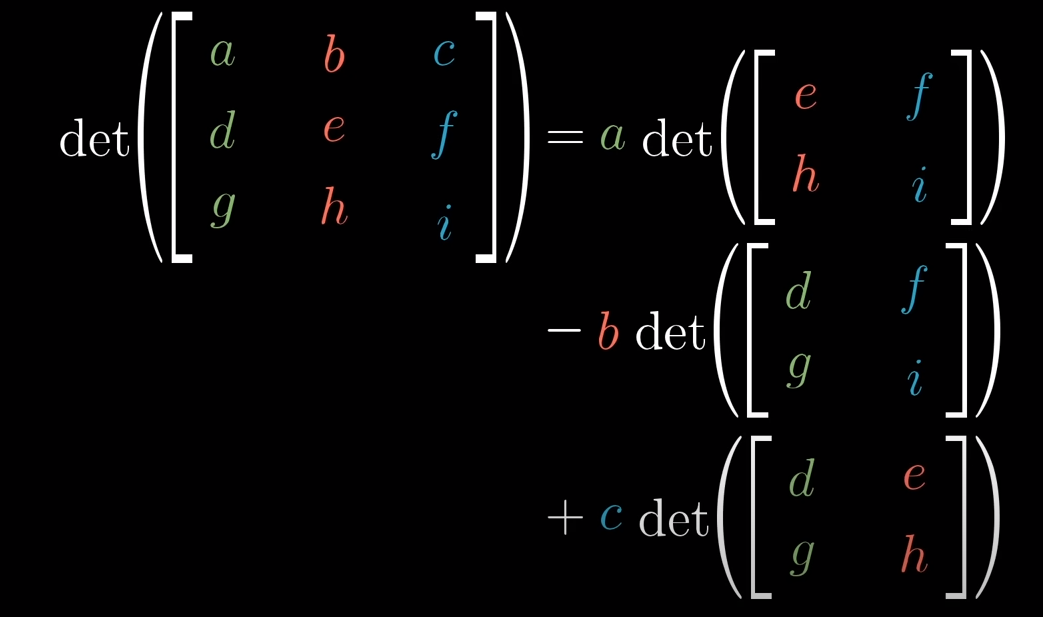
Dot products

• Multiply corresponding elements of vector
• Sum resulting coefficients/amplitudes
• Amplitudes that don’t exist are 0, and multiplication rule holds true

$$a=3j+2k,b=2j$$ $$a\cdot b=(3\ast 2)$$

Other rules

Vectors are orthogonal when their dot product is zero

$$a\cdot b=|a||b|cos(\theta )$$

$$a\cdot a=|a{|}^2$$

General or Non-Conforming Rules

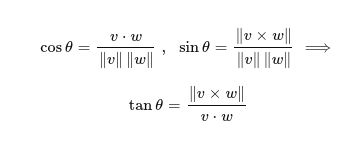
Angles between vectors

$$co{s}^{-1}(\frac{|{\vec{V}}_x|}{|\vec{V}|})={\theta }_{Vx}$$

The inverse cosine of the x component of the vector over the magnitude of the vector gives the angle to the x axis.

Any two Vectors:

$$\theta ={\cos }^{-1}\left(\frac{\mathbf{A}\cdot \mathbf{B}}{|\mathbf{A}||\mathbf{B}|}\right)$$

Verify Orthogonal: Vectors are orthogonal if their dot product is equal to zero.